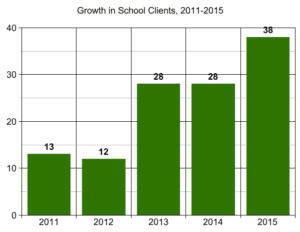
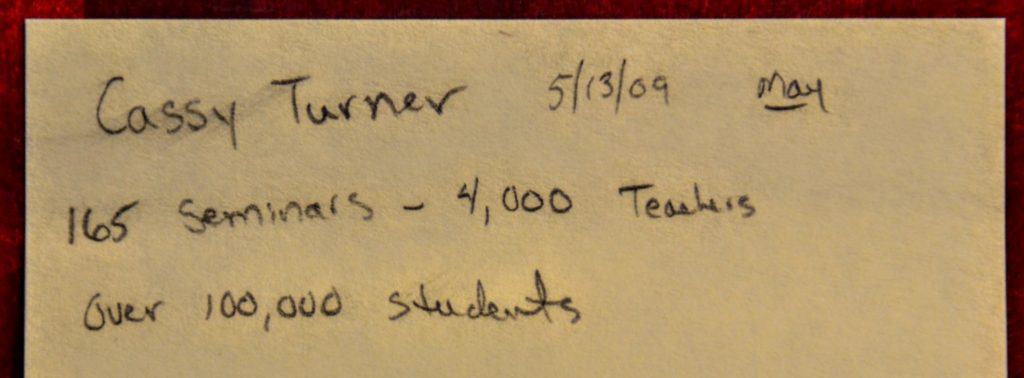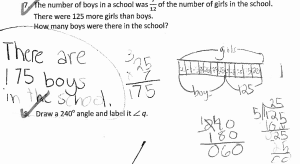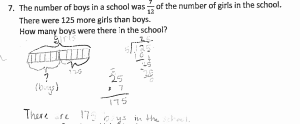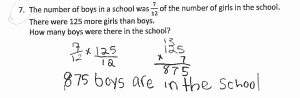Cassy Turner – Page 16

Reader Survey: Help Us Help You

August 1, 2016 by Cassy Turner 1 Comment

As the popularity and influence of Singapore Math® programs grow, so does interest in focused professional development around Singapore-based concepts.

Each month, we receive dozens of inquiries from teachers and schools seeking training to ensure that they are using the curriculum as effectively as possible. We are in the process of planning future educational programs for teachers and schools, and would love to know how we can help you!

If you are interested in learning more about Singapore Math or taking your current math teaching skills to a higher level, please take a few minutes to complete this survey.

Online survey powered by Typeform

Filed Under: Math Events, Tales from the classroom, Training

Great Math News from City Springs School In Baltimore

May 24, 2016 by Cassy Turner Leave a Comment

For the last year, I’ve been working with City Springs Elementary/Middle School in Baltimore. Here’s a short description from the school’s website:

City Springs Elementary/Middle School is a neighborhood charter school operated by the Baltimore Curriculum Project (BCP). We are a conversion charter school, which means we were an already existing Baltimore City Public School that was taken over by an outside operator to bring innovative and research-based curriculum and other programs to enhance the school. To learn more about BCP, click here.

Initially, the school was seeking help with its Middle School math. After I made a pair of on-site visits at the end of the 2014-2015 school year, Dr. Rhonda Richetta, Principal of City Springs, decided to adopt Singapore’s Primary Mathematics Common Core Edition.

I’ve returned to City Springs periodically this year to provide continuing support as the school’s teachers and coaches adopted a Singapore Math® curriculum. The school is making remarkable progress, and I want to share stories written by some of City Springs’ dedicated teachers about the students’ growth during the year.

I’ve clipped an excerpt from each story with teachers’ observations and very valuable insights about the program and why it is working so well for their students. Please click on the links to read complete stories from the school’s website. I love the photos of students showing off their skills and having fun with math!

Ms. Schoenleber: Introducing Singapore Math (November 2015) “Classroom manipulatives have helped our kids get better at problem solving and justifying their answers for tough math problems.”

Ms. Hagemann: It’s More than Just a Game (November 2015) “One way to get stronger in mental math is by use math-based games to reinforce basic concepts and encourage mathematical thinking…Students in Ms. Hageman’s class love mental math games!”

Ms. Smith: Moving Ahead in Mathh (February 2016) “Singapore Math has been very challenging but it has also been very rewarding, and they have especially loved the use of manipulatives in class.”

Ms. Barry: Stepping Up to the Ratio Challenge (February 2016) “Ratio problems can be really tricky. Sometimes these multi-step problems are so challenging that we spend 15, 30, or even 45 minutes on one problem! Our students love to rise to the challenge, and have grown so much in their math skills with these complex problems.”

Ms. Barry’s also class wanted to challenge readers to solve a ratio problem they worked on. How did you do?

Ms. Lineberry: Introducing Fractions (May 2016) “At first, we struggled to figure fractions out. Trying to wrap our minds around halves and fourths proved difficult at first. Things became a little clearer after we started using “manipulatives,” hands-on objects used to illustrate math concepts.”

Ms. Williams: Knowing All the Angles (May 2016) “Students began their geometrical journey by learning how to measure angles…Later, they will start learning to measure geometric angles made by two lines emanating out of the center of a circle, and eventually beginning exploring the complex world of geometry formulas.”

Working with City Springs has been one of the most rewarding and enjoyable assignments of my career. Teachers have embraced the challenge of adopting a new program and students are making wonderful progress. I can’t wait to see their growth in Year Two! Thank You, City Springs!

[Full disclosure: My work assignment at City Springs is contracted through Staff Development for Educators.]

Filed Under: Math Resources, News, Schools, Tales from the classroom, Training Tagged With: adopting Singapore math materials, School News, Singapore Math curriculum, Singapore Math training, tales from the classroom

Meet Beth Curran, Singapore Math® Trainer

May 17, 2016 by Cassy Turner 2 Comments

In 2008, I left teaching in the classroom to champion Singapore Mathematics and expand its reach to elementary schools and children everywhere. Looking back on the past eight years, I am amazed by the incredible opportunities I’ve had to help schools and teachers make math from Singapore work for every child in every classroom.

Demand for my training and coaching services has grown every year; recently, it has become impossible to accommodate all the schools looking for help with their math instruction.

Expanding has been on my radar for several years, but I did not want growth to affect the quality of professional development services. To take this important step, I needed a candidate who has stellar credentials as a teacher/trainer/coach AND who shares my passion for elementary math.

I’m delighted to share some exciting news. After eight years as a one-person consultancy, I am hiring my first employee.

Introducing Beth Curran

In a 13-year career, Beth Curran has taught mathematics in Kindergarten through 4th Grade as both a classroom teacher and a Singapore Math® specialist. Beth is currently the Lead Math Teacher and Math Department Chair at St. Anne’s-Belfield School, an independent Pre-K-12 school in Charlottesville, Virginia. At St. Anne’s, she oversaw the successful adoption of Primary Mathematics, guiding a team of teachers and partnering with administrators and parents.

Beth wrote about the St. Anne’s implementation here.

What do Beth’s Colleagues say about her impact?

The transition for our faculty to Singapore Math was daunting at first. The unknown can always challenge teachers and schools. Yet, Beth, as a member of a team of newly-minted math specialists, provided key expertise and wise counsel to her colleagues. The result was a palatable sense of relief as the new math vision was manifested daily by strong instruction. She enabled our teachers and school to move confidently in this new direction.
– Fred Chandler, Associate Head of School for Academics, St. Anne’s – Belfield School

There is a depth to Beth Curran’s teaching, and–through her example and through many discussions–she has helped me deepen my own teaching. She prioritizes true mastery of worthy concepts.
– Karen LeMaire, Kindergarten through 4th Grade Math Specialist, St. Anne’s – Belfield School

Beth has provided professional development and ongoing support services to other Virginia schools that have implemented Singapore Math curricula, as well as hosting several informational sessions to schools interested in the Singapore approach. In addition, she has presented at State and regional math educator conferences. Beth is a dedicated, award-winning teacher, presenter, mentor and advocate of making quality mathematics education accessible to all students.

Beth says, “I’m so excited to share all that I’ve learned on my own Singapore Math journey with educators throughout the country, and beyond.”

I’m thrilled that Beth will be joining me in June. Welcome to the team, Beth!

P.S. In addition to hiring Beth, I’ve also formed a new company, Math Champions Professional Development, LLC. More on that development coming soon.

Filed Under: News, Training

4,000 Teachers, 100,000 Students: Celebrating 7 Years with BER

May 12, 2016 by Cassy Turner 2 Comments

In 2008, I left teaching in the classroom to champion Singapore Mathematics and expand its reach to elementary schools and children everywhere. The following year, the Bureau of Education and Research (BER) gave me an amazing opportunity to pursue this goal by presenting Singapore Math workshops throughout North America.

Some attendees at my BER seminars came with prior knowledge about the Singapore curriculum, but a bigger number were being introduced to Math from Singapore for the first time.

At a Seattle workshop earlier this year, BER’s Mark Ita surprised me (and other attendees) by presenting me with a handsome plaque, which read, in part:

In Recognition of Your Distinguished Teaching and Your Outstanding Contribution to the Education Profession

4,000 Teachers, 100,000 Students

The stats scribbled on a Post-It Note on the back of the plaque included some tangible data to support this statement:

165 Seminars
4,000 Teachers
Over 100,000 Students

Cassy with BER’s Mark Ita

It is highly satisfying to know that I have impacted this number of teachers and students through my BER presentations. On the other hand, the National Center for Education Statistics reports that there are about 35.2 million Pre-K to Grade 8 students in the United States. Clearly, there is much more work to be done!

I am very grateful to BER for giving me the opportunity to present Singapore Math workshops on their behalf over the past seven years. Sincere thanks to Rich, Boyce, Mark, Nargis, Lisa and the entire travel logistics team, and the dozens of project managers who have provided encouragement and support along the way. Thank you so much!

Filed Under: Math Events, Math Resources, Training Tagged With: BER, Math Sprints, Model Method, Professional development, Singapore Math curriculum, Singapore Math training, Singapore Math word problems, tales from the classroom

Bar Model Solutions – by Students

April 12, 2016 by Cassy Turner 2 Comments

After the post on Assessing Bar Model Solutions went up, Beth Curran sent a message: “We just did that problem!” She agreed to share some student work: