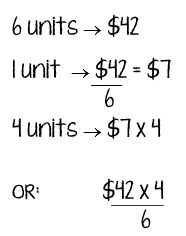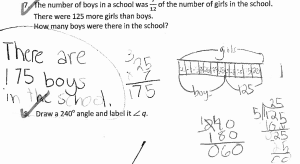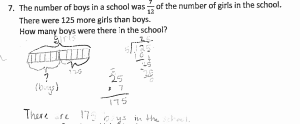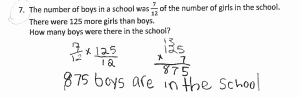Word Problem

What’s the Word Problem?

December 9, 2019 by Cassy Turner 2 Comments

I often work with international Schools where the teachers commit to two-three years and then move on to other schools and other countries. I was surprised by an email this week from a former 3rd-grade teacher I worked with at a school in China. She is now teaching in Malaysia.

Hi Cassy, I’ve moved on…but all that bar model training is serving me well at the math PD at my new school!

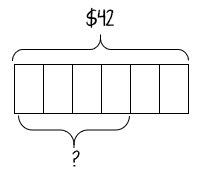
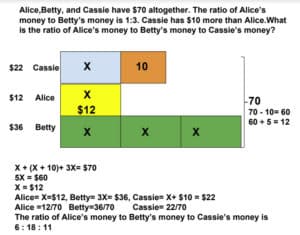
She included this image:

Can you write a word problem for this bar model and the calculations?
What grade level might this be from?
What do you notice about the manipuative used?
What questions can we ask based on the model given?

Filed Under: Math Resources, Tales from the classroom Tagged With: Bar model, Word Problem

Word Problem Wednesday – Rulers and Bread

June 6, 2018 by Cassy Turner Leave a Comment

Word Problem Wednesday was such a hit, we’re going to continue throughout the year with one problem a month.

This problem popped up in my Medium feed last month:

Algebraic expressions — the return! Guess the Misconception author Craig Barton noted that on a quiz website for test prep in the UK, only 1 in 3 students could answer this problem correctly. At the time, I was also analyzing the value of model drawing by reviewing released problems from the 6th-grade STAAR tests, so my first thought was, hmm, how would this work as a bar model?

Pretty well, actually. If I know that:

I can find:

The AQA is an independent education charity that offers GCSE testing in the UK. DiagnosticQuestions.com provides multiple choice questions so you can build your own assessment, or use one of their collections.

Check out a bar model solution:

Finally, this month’s problem comes from the Grade 6 STAAR 2013-2017 Released Test questions from lead4ward aligned to the Texas Essential Knowledge and Skills or TEKS. It aligns to the standard:

6.4(B) (New) Proportional Reasoning: Apply qualitative and quantitative reasoning to solve prediction and comparison of real-world problems involving ratios and rates.

There are 176 slices of bread in 8 loaves. If there are the same number of slices in each loaf, how many slices of bread are there in 5 loaves?

Submit your solutions by the end of the month!

The prior problem was from the Teacher’s Guide for Primary Mathematics US Edition 5A.

We had a couple of submissions.

Here’s Shirley Davis’ model and algebra combo:

Filed Under: Math Resources, Word Problem Wednesday Tagged With: TEKS, Word Problem, Word Problem Wednesday

Throwback Thursday – Bar Model Solutions – by Students

August 24, 2017 by Cassy Turner 1 Comment

Over the summer, we thought it would be fun to run some of the most popular posts from the past. It’s always interesting to see how students’ minds work. When I re-read a post from the past I always take away something different because I am in a different place with my own experience. Perhaps you are as well!

Bar Model Solutions – by Students!

Originally published 4/12/2016

After the post on Assessing Bar Model Solutions went up, Beth Curran sent a message: “We just did that problem!” She agreed to share some student work:

And when the students didn’t draw a model:

I see this as a comparison problem:

5 units -> 125 students
1 unit -> 125 ÷ 5 = 25
7 units for boys -> 7 x 25 = 175 boys in all

(That’s the Thinking Blocks Model Drawing tool that allows you to insert your own word problems and solve – or you can use the pre-made questions!)

Filed Under: Math Resources, Tales from the classroom Tagged With: Model Method, Singapore Math word problems, Word Problem

Word Problem Wednesday – Pears and Oranges

June 21, 2017 by Cassy Turner 2 Comments

Summer’s here, but you’re missing your math? Don’t despair – we’ve got you covered. Check the site each week for one whopper of a word problem that’s sure to challenge!

This week’s problem comes from Challenging Problems in Primary Schools – Intermediate by Dr Y H Leong, published in 2004 by SNP Panpac Pte Ltd.( Intermediate is for students in Primary 4 and 5.)

3 pears and 4 oranges cost $3.80. If 1 pear and 1 orange together cost $1.10, find the cost of 1 pear.

Submit your solutions and we’ll post all interesting strategies next week.

Last week’s problem and solution:
Gavin has 356 cards. He has 286 more cards than Howie. How many cards must Gavin give to Howie so that they both have the same number of cards?