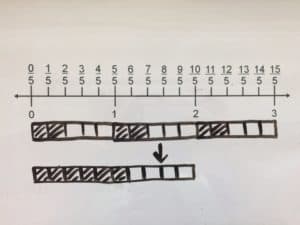
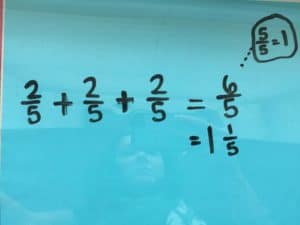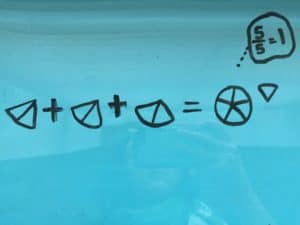This month’s Word Problem Wednesday problem comes from an article in the Daily Express, a UK newpaper.
The headline teases: This is the maths puzzle that is baffling everyone – but could you solve it?
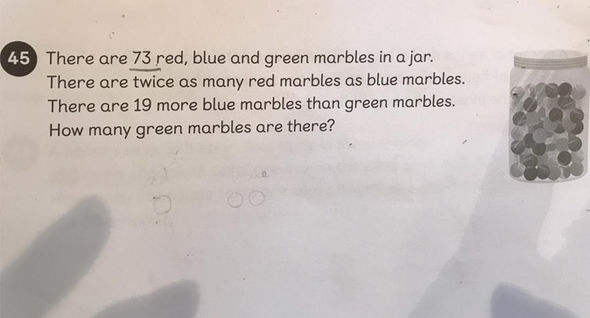
Yes, we can! So, don’t lose your marbles over this one.
This appears to come from a Maths No Problem! workbook, probably 2A as the article states it is a problem for 7-year-olds. The author interviews a math professor:
Math expert, Dr. James Hind, of Nottingham Trent University, said the confusing question is above the level it was set for and to reach a conclusion it is best to try a number of equations.
Dr. Hind then proceeds to use a guess and check method to solve the problem. Maybe they asked the wrong expert.
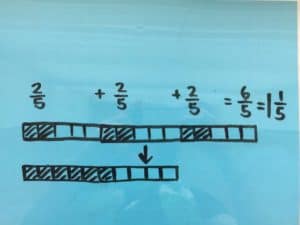
Programs based on a Singapore Math approach start bar model drawing in either 2nd or 3rd grade, making this a challenging problem for many 2nd graders, but not a guess and check problem. Visualization of problem-solving actually starts in kindergarten!
See if you can solve this one like a 7-year- old. Submit your solutions by the end of the month!
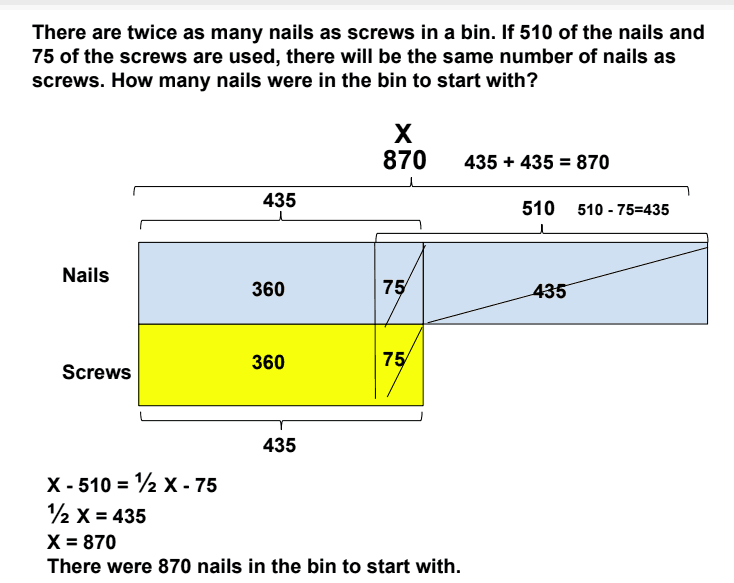
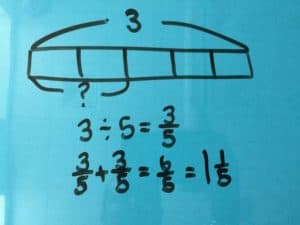
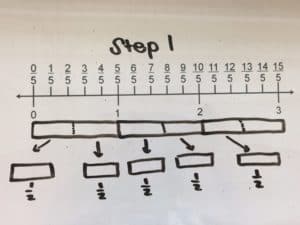
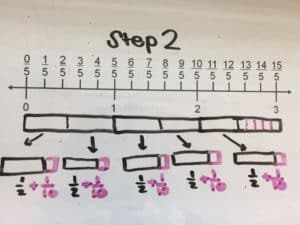
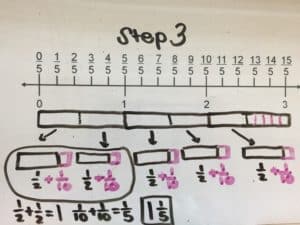
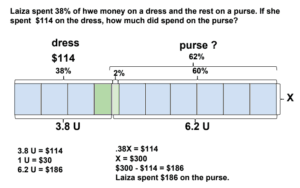
Our last Word Problem Wednesday problem was from the chapter on the “Model Method and Algebra” from The Singapore Model Method for Learning Mathematics.
We had several correct answers submitted. Here’s a worked example from Shirley Davis:
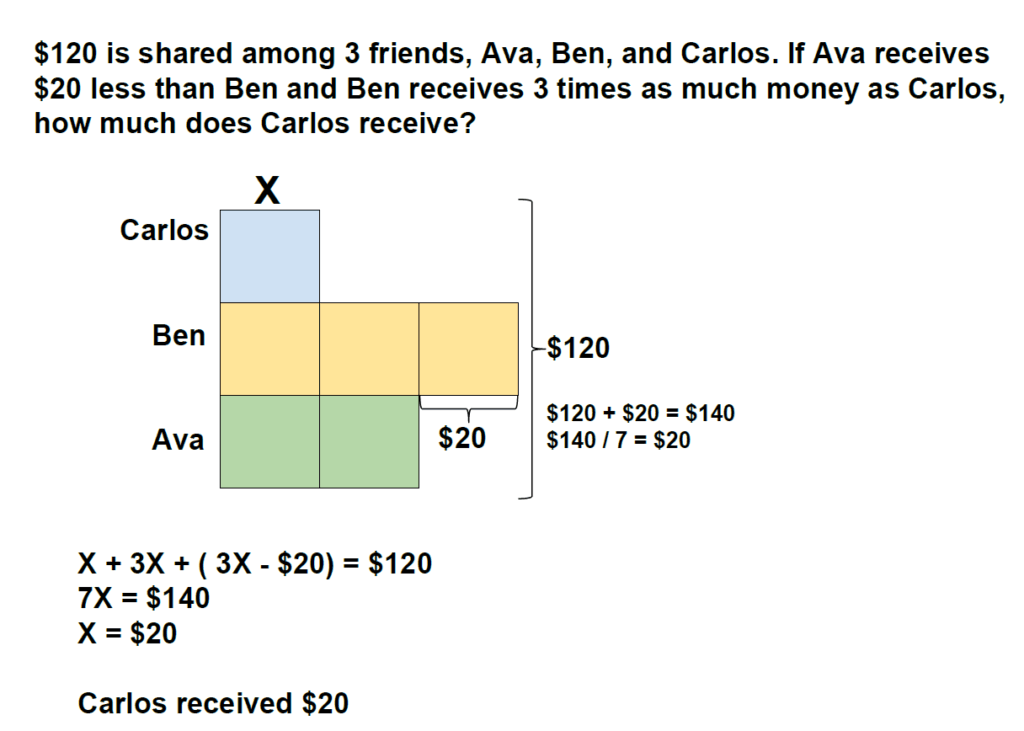
How did you do?