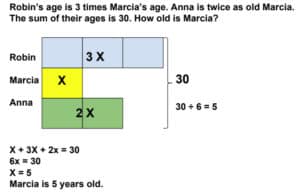
This month’s problem comes from the website TestPapersFree.com, which provides past copies of continual and semestral assessments from Singapore Primary Schools. This is a great resource if you’re looking to see questions directly from Singapore classrooms. This problem is from Raffles Girls School, Grade 4, and is a Semester 2 assessment, which is the final term of the year.
This month’s problem comes from the website TestPapersFree.com, which provides past copies of continual and semestral assessments from Singapore Primary Schools. This is a great resource if you’re looking to see questions directly from Singapore classrooms. This problem is from Raffles Girls School, Grade 4, and is a Semester 2 assessment, which is the final term of the year.
Pei Ling had 3 times as many cards Zandy.
Sulaiman had half the number of cards Zandy had.
There were a total of 1278 cards.
How many more cards did Pei Ling have than Zandy?
Submit your solutions by the end of the month!
The prior problem was from the Grade 6 STAAR 2013-2017 Released Test questions from lead4ward aligned to the Texas Essential Knowledge and Skills or TEKS.
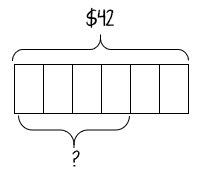
There are 176 slices of bread in 8 loaves. If there are the same number of slices in each loaf, how many slices of bread are there in 5 loaves?
How did you do?