Word Problem Wednesday was such a hit, we’re going to continue throughout the year with one problem a month.
This problem was taken from Noetic Learning’s problem of the week and builds on the problem with the ropes from last month. Sign up to receive their weekly problems.
Robin’s age is 3 times Marcia’s age. Anna is twice as old as Marcia. The sum of their ages is 30. How old is Marcia?
Submit your solutions and we’ll post all interesting strategies.
This problem was taken from Challenging Word Problems 2, a supplement to the Primary Mathematics series:
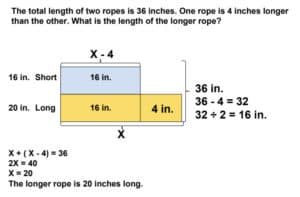
The total length of two ropes is 36 in. One rope is 4 in. longer than the other. What is the length of the longer rope?
Dedicated reader, Shirley Davis submitted the following solution: