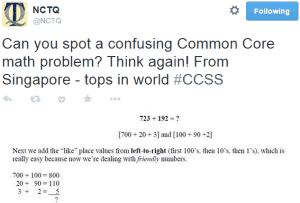
“The Internet Is Losing It Over This Second Grade Math Problem,” reads the headline from an article posted online by msn.com. The article goes on to support the student’s mother’s conclusion that, “this isn’t exactly a question most 8-year-olds would understand.”
“The Internet Is Losing It Over This Second Grade Math Problem,” reads the headline from an article posted online by msn.com. The article goes on to support the student’s mother’s conclusion that, “this isn’t exactly a question most 8-year-olds would understand.”
The problem reads, “There are 49 dogs signed up to compete in the dog show. There are 36 more small dogs than large dogs signed up to compete. How many small dogs are signed up to compete?”
Yes, this is that “new” math. This is the math that second graders will need to succeed as adults. Gone are the days when correctly completing 20 addition or subtraction problems is enough. Problem-solving and logical thinking is what employers are looking for. So, yes, this is a challenging problem, but not a problem we should be avoiding in our schools simply because the internet says it’s too hard.
I agree there is a flaw in this problem, but it’s not in the problem itself, it’s in the numbers that were chosen. Fortunately, the numbers are the least important part of solving a word problem. That stands worthy of repeating. The numbers are the LEAST important part of solving a word problem.
So, what is then? Visualization and comprehension!
Students need to visualize the problem and then represent it with models or pictures. This is why teaching bar modeling is so very important in the early grades.
Here’s a video that shows how easy it is to solve this problem if you focus on visualization first.
Any good teacher will follow up a lesson with practice, so here is your Word Problem Wednesday for February.
This problem was taken from Challenging Word Problems 2, a supplement to the Primary Mathematics series:
The total length of two ropes is 36 in. One rope is 4 in. longer than the other. What is the length of the longer rope?
Submit your solutions and we’ll post all interesting strategies.
The previous problem came from i-Excel Heuristic and Model Approach Primary 5 by Li Fanglan published by FAN-Math:
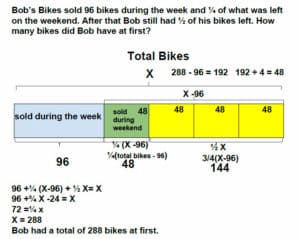
Bob’s Bikes sold 96 bikes during the week and 1/4 of what was left on the weekend. After that, Bob still had 1/2 of his bikes left. How many bikes did Bob have at first?
Dedicated readers submitted the following solutions, first an image from Shirley Davis:
And a video from Kristine Simonson, who has been using some of the problems with her fourth graders: