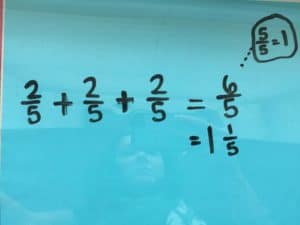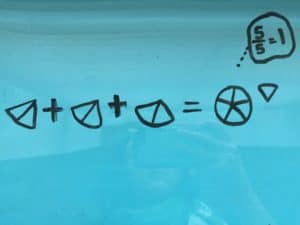This month’s Word Problem Wednesday problem comes from the chapter on the “Model Method and Algebra” from The Singapore Model Method for Learning Mathematics.
This month’s Word Problem Wednesday problem comes from the chapter on the “Model Method and Algebra” from The Singapore Model Method for Learning Mathematics.
The book models the Unitary Method as well as 3 variations on an algebraic solution. The author’s end this problem with the following commentary
The Model Method is a means, not and end in itself. It helps students formulate an algebraic equation to solve the problem. While more able students can proceed quickly to the absract algebraic method to solve problems without drawing a model, others may still need to rely on drawing the model as a problem-solving heuristic.
-The Singapore Model Method for Learning Mathematics, p. 58
Wise words, indeed! On to the problem:
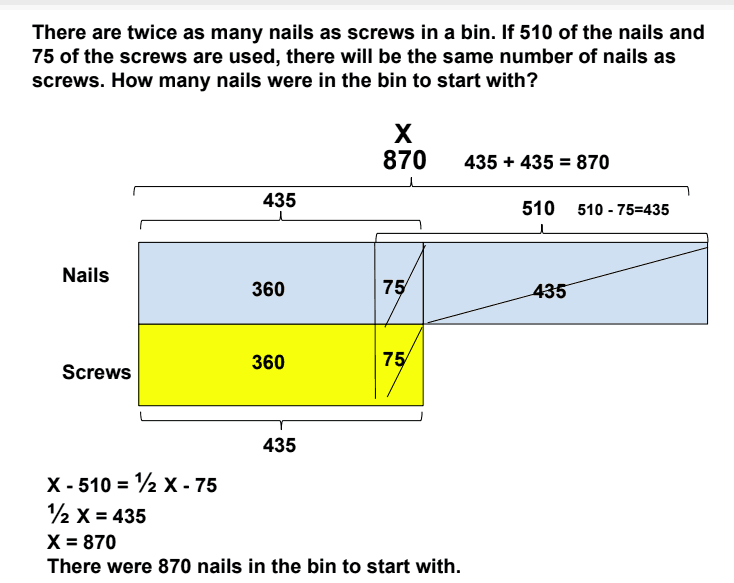
$120 is shared among 3 friends, Ava, Ben, and Carlos. If Ava receives $20 less than Ben, and Ben receives 3 times as much money as Carlos, how much does Carlos receive?
Submit your solutions by the end of the month!
Last month’s Word Problem Wednesday problem was from the chapter on Real-World Problems Math in Focus 2A:
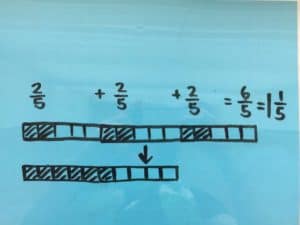
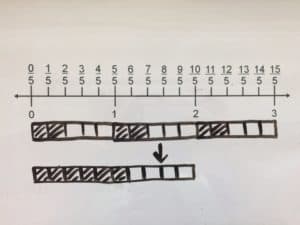
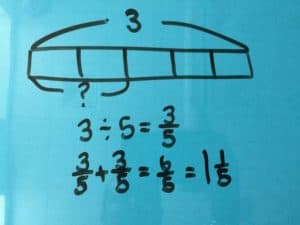
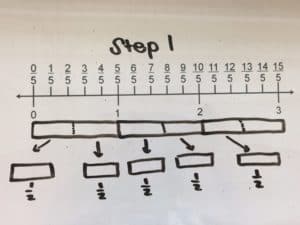
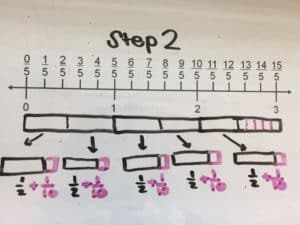
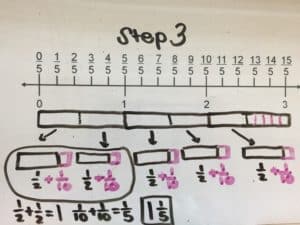
We had several correct answers submitted. Here’s a worked example from Minnesota math teacher and coach Kris Simonsen:
How did you do?