Math Resources

Giving Thanks – 2019 Year in Review

January 6, 2020 by Cassy Leave a Comment

As December brings a break for holidays and the start of a new year, we appreciate the opportunity to spend quality time with friends and family. During this pause, I also reflect on our past year working with schools and teachers and plan for the year ahead.

Reflecting on 2019, I am reminded of my great good fortune to have discovered my calling. Last year, I celebrated my 12th year as a mathematics trainer/coach/consultant and 17^th year working with Singapore Mathematics programs. I am so grateful for the opportunity to champion elementary math education AND to be able to spend time so much time in classrooms with teachers and students. I TRULY LOVE my job.

I say this every year, and it continues to be true: I am humbled and honored that schools seek out our services year after year. We extend our sincere thanks to schools that hired us in 2019 and each of the 200+ clients we have served over the past dozen years.

Before everyone returns to their daily routine, we wanted to share with you some highlights and achievements that Math Champions celebrated in 2019.

Training/Coaching/Consulting

Over the past year, we worked with schools from coast-to-coast (and abroad) in all manner of roles: overseeing new curriculum adoptions, coaching teachers, coaching coaches, advising administration, and more. We also developed hybrid programs, crafted to meet the particular needs of schools seeking a custom solution.

In 2019:

38 schools hired Math Champions to help improve their math instruction.
28 of those schools (more than 73%) were repeat clients.
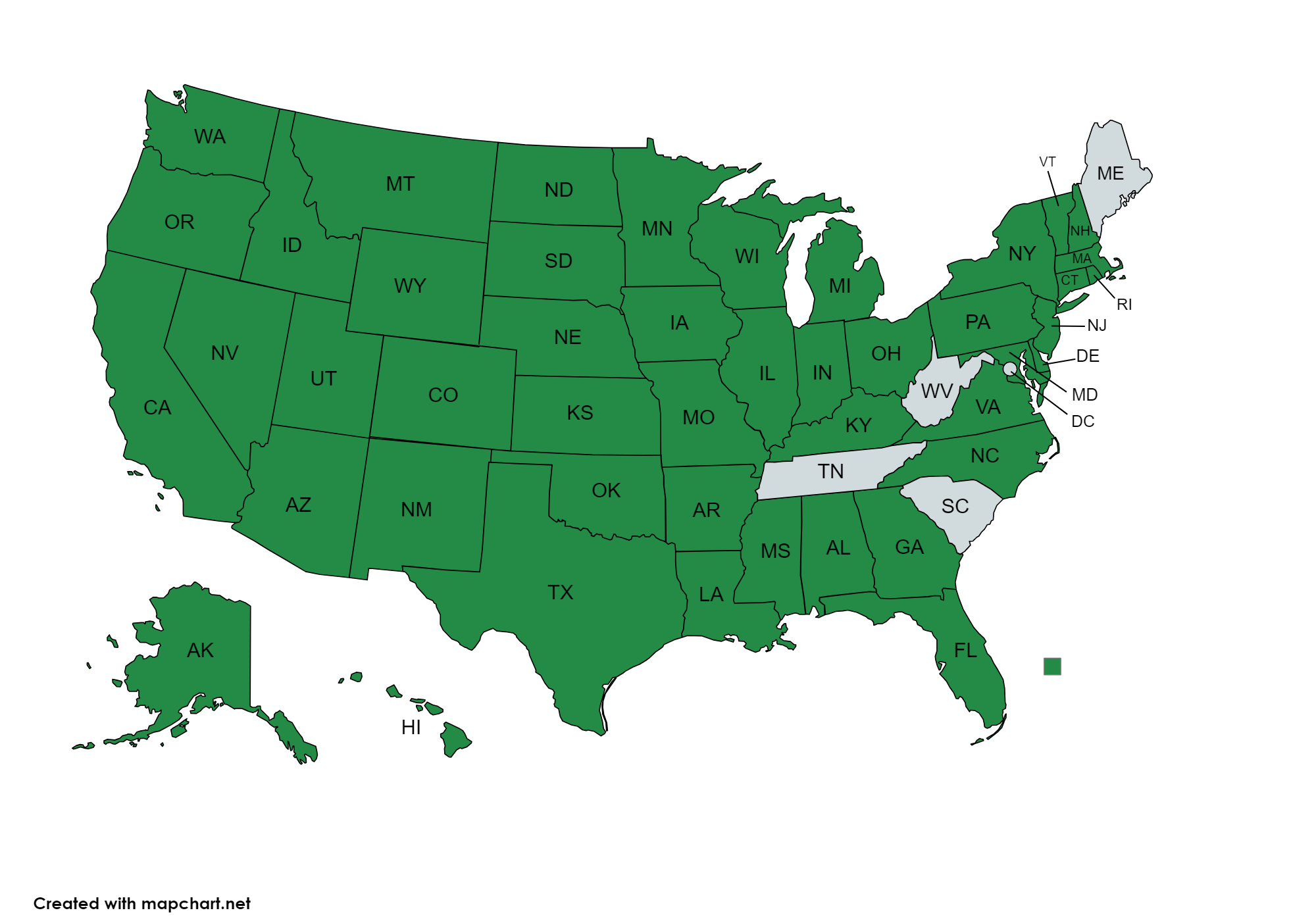
We visited schools in 15 States as well as several schools abroad (more on these below).
Language immersion and Singapore Math were a great match! We worked with Mandarin, Spanish, French, German, and Italian immersion schools.

Although we love to visit schools on any occasion, it is especially gratifying when we have the opportunity to observe the significant progress that schools make on return visits!

International Training

We began 2019 in Guam, completing our first teacher training assignment under a multi-year contract with the Department of Education. Collectively, we spent more than a month on the island in January and May helping more than 400 teachers and DOE staff learn about the Singapore approach to math instruction. We look forward to returning in 2020.

Twenty-nineteen also featured a training trip to China. We returned (for a fourth time!) to Hangzhou International School and made our first visit to Georgia School of Ningbo. In China, as a non-Mandarin speaker, getting there is half the fun. It seemed like we spent an hour trying to find the ticket office at Hangzhou East Railway Station. But why worry, as inter-city trains depart every 15 minutes! When finally aboard, the high-speed rail ride between Hangzhou and Ningbo, with speeds exceeding 300 km/h, was thrilling.

In 2019, Math Champions was awarded its second contract in three years to assist the Republic of Palau’s Ministry of Education with its Singapore Math program. In January 2020, we will return to Palau to spend two weeks with more than 200 of the nation’s teachers.

Dimensions Math in the Wild!

In 2018, we celebrated the launch of Dimensions Math, a new Pre-K to Grade 5 series based on the pedagogy and methodology of math education in Singapore.

As the lead author of Dimensions Math Teacher’s Guides for K-5, it was super exciting and gratifying to work with schools using Dimensions in 2019. I look forward to the completion of the Dimensions Math series in 2020.

Jumpstart Your Singapore Math Instruction

Jumpstart is our two-day interactive, introductory workshop on how to best use the Singapore Math approach. In 2019, we finally realized the goal of offering Jumpstart in locations from coast-to-coast. Hundreds of teachers (including several from abroad) attended sessions presented in Virginia, Arizona, Minnesota, Colorado and California.

Presentations at National Educator Conferences

Again in 2019, we were busy attending annual conferences for math educators (our continuing education). In addition, we were honored to present at the following conferences:

National Council of Teachers of Mathematics (NCTM)
National Council of Supervisors of Mathematics (NCSM)
National Catholic Educators Association (NCEA)
Minnesota Council of Teachers of Mathematics (MCTM)
California Mathematics Council-South (CMC-S)

MILE-stones

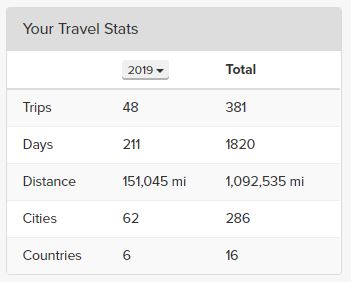
According to TripIt, I established a new record with 151,045 miles flown in 2019. In addition, I topped 1 million miles for the period from 2008-present. [OK, I admit that there are some personal trips counted here. Still…].

Looking ahead

Whew. What a year!

What does 2020 hold in store? Here are some of the things we’re looking forward to in the year ahead:

Working with returning and new school clients. Did I say that I LOVE spending time in classrooms with teachers and students?
Presenting Jumpstart Your Singapore Math workshops across the USA and (new in 2020) Canada.
Presenting at and attending NCTM, NCSM, MCTM, CMC and other educator conferences.

Finally, I want to extend special thanks to our favorite partners/friends:

And thank you to our fabulous Jumpstart 2019 host schools:

Faith Christian School – Roanoke, VA
Benchmark School – Phoenix, AZ
Golden View Classical Academy – Golden, CO
Mounds Park Academy – Saint Paul, MN
Irvine Hebrew Day School – Santa Ana, CA

Filed Under: Math Resources, Thanks Tagged With: Giving Thanks

What’s the Word Problem?

December 9, 2019 by Cassy 2 Comments

I often work with international Schools where the teachers commit to two-three years and then move on to other schools and other countries. I was surprised by an email this week from a former 3rd-grade teacher I worked with at a school in China. She is now teaching in Malaysia.

Hi Cassy, I’ve moved on…but all that bar model training is serving me well at the math PD at my new school!

She included this image:

Can you write a word problem for this bar model and the calculations?
What grade level might this be from?
What do you notice about the manipuative used?
What questions can we ask based on the model given?

Filed Under: Math Resources, Tales from the classroom Tagged With: Bar model, Word Problem

Graphing the Holidays

November 14, 2019 by Cassy Leave a Comment

Originally posted 11/27/2018

Teaching between Thanksgiving and the winter break can be a challenge. How do you keep your students engaged in meaningful math learning while embracing the season? Introducing graphing and data analysis might just be the answer.

Imagine starting your day in first grade with a question about favorite holiday treats. Students can answer the question and instantly you have meaningful data that can be organized into a tally chart, picture graph, or bar graph for students to analyze. Or, students can build a bar graph with post-it notes as they make their choices. Then, spend some time analyzing the results.

Ask 5th graders if they traveled over Thanksgiving break. If so, how far? Now use this data to find mean, median, and mode, or to create a histogram for students to analyze. Or, chart the temperatures over the course of a couple of weeks and use this data to create a line graph.

Third and fourth graders could tally the number of candles in their homes for the holidays and use this data to create a line plot. Fourth graders can use their line plots to explore finding the median.

Planning a holiday party? Survey the students on what should be served and what activities should be included. Students can present the findings in a graph and use the results to determine how much and what needs to be donated or purchased to make the party a success.

The holidays are a great time to share family traditions. Why not use that information to meet some graphing and data analysis standards?

For other ideas to keep students engaged in learning read Mental Math Breaks from December 2017.

Filed Under: Math Resources, Tales from the classroom Tagged With: grade2, grade3, grade4, grade5, grade6, Singapore Math curriculum, teaching ideas

Who’s doing the talking?

September 17, 2019 by Beth Curran 2 Comments

A new school year brings new commitments to improving our practice as teachers of mathematics. One tip I often share with the teachers I coach is, “Ask more and tell less.” Well, that’s easy to say, but what does that look and sound like in the classroom?

Often times, the teacher’s guides are written following a more traditional, lecture-style of teaching. They encourage the teacher to model, or work problems, while the students watch, and then the students are asked to mimic what the teacher did with a similar problem. I challenge you to flip the script and replace the word “show” with “have the students model” and replace “tell” with “ask”. When your teacher’s guide says to show the students the difference or similarities between problems or concepts replace that with, “ask the students what they notice?” It’s these little tweaks that will go a long way toward engaging your students in meaningful discourse and ultimately deepening their understanding.

A fourth-grade teacher from Aurora, Colorado shared her strategies for engaging students in math talk in her classroom.

While this appears to be written for the students to follow, it also suggests some great questions for teachers to ask to generate more discussion.

As students are working through a task ask:

How did you solve that?
How do you know that’s correct?
Can you solve it another way?
Can you build a model?
Can you use numbers and symbols to explain your model?
Is that the best (most efficient) way to solve that?
Is your answer reasonable?
Do you agree or disagree with your partner’s answer?

So, who’s doing all the talking? Give some of these questions a try and let us know how it goes.

Filed Under: Math Resources, Tales from the classroom, Training Tagged With: Math Talk, tales from the classroom, Tips

Word Problem Wednesday – Marbles

March 20, 2019 by Cassy 3 Comments

This month’s Word Problem Wednesday problem comes from an article in the Daily Express, a UK newpaper.

The headline teases: This is the maths puzzle that is baffling everyone – but could you solve it?

Yes, we can! So, don’t lose your marbles over this one.

This appears to come from a Maths No Problem! workbook, probably 2A as the article states it is a problem for 7-year-olds. The author interviews a math professor:

Math expert, Dr. James Hind, of Nottingham Trent University, said the confusing question is above the level it was set for and to reach a conclusion it is best to try a number of equations.

Dr. Hind then proceeds to use a guess and check method to solve the problem. Maybe they asked the wrong expert.

Programs based on a Singapore Math approach start bar model drawing in either 2nd or 3rd grade, making this a challenging problem for many 2nd graders, but not a guess and check problem. Visualization of problem-solving actually starts in kindergarten!

See if you can solve this one like a 7-year- old. Submit your solutions by the end of the month!

Our last Word Problem Wednesday problem was from the chapter on the “Model Method and Algebra” from The Singapore Model Method for Learning Mathematics.