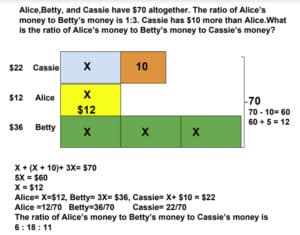
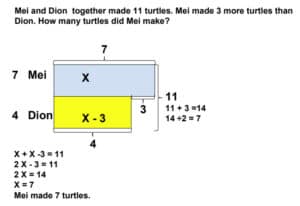
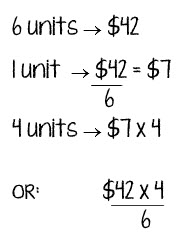This month’s Word Problem Wednesday problem comes from Math in Focus Grade 3.
Farmer Fred makes 4 quarts of orange juice on Monday. He makes 2 quarts more orange juice on Tuesday than on Monday. He makes 2 more quarts on Wednesday than on Tuesday. He carries on making 2 more quarts of orange juice every day than the day before. In how many days will he make a total of 80 pints of orange juice?
Submit your solutions by the end of the month!
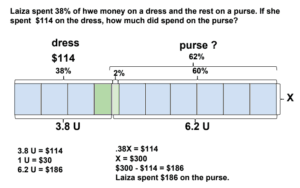
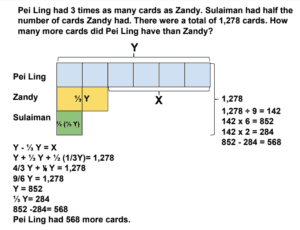
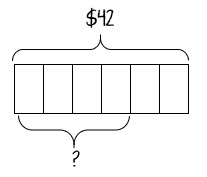
Last month’s problem was from Primary Mathematics Challenging Word Problems 3:
How did you do?




 This option works great if you have enough discs for each student to have 20 of each place value; 20 ones, 20 tens, 20 hundreds, etc. Students are expected to keep these baggies or boxes of discs in their desks.
This option works great if you have enough discs for each student to have 20 of each place value; 20 ones, 20 tens, 20 hundreds, etc. Students are expected to keep these baggies or boxes of discs in their desks.
 In this case, discs are organized by place value into tubs. So, you would have a tub of ones, a tub of tens, and so on. In each tub, you can keep a set of small cups (Dixie cups work well) for students to take a scoop of the discs when needed. Clean up is a snap. Students simply dump the cups of discs back into the correct place value tub.
In this case, discs are organized by place value into tubs. So, you would have a tub of ones, a tub of tens, and so on. In each tub, you can keep a set of small cups (Dixie cups work well) for students to take a scoop of the discs when needed. Clean up is a snap. Students simply dump the cups of discs back into the correct place value tub. Community Tubs
Community Tubs










 Kindergarten – used for counting with one-to-one correspondence, measuring with non-standard units, and for modeling basic addition and subtraction situations.
Kindergarten – used for counting with one-to-one correspondence, measuring with non-standard units, and for modeling basic addition and subtraction situations. Find Base Ten Blocks
Find Base Ten Blocks 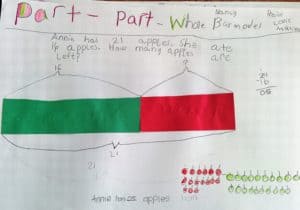
 Find number cards on our
Find number cards on our