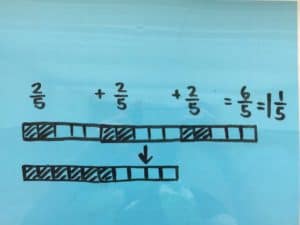
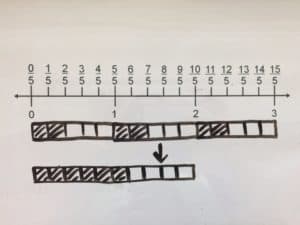
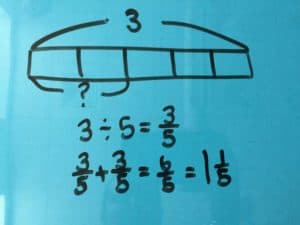
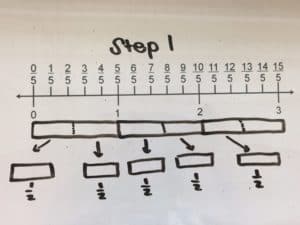
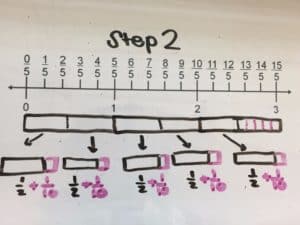
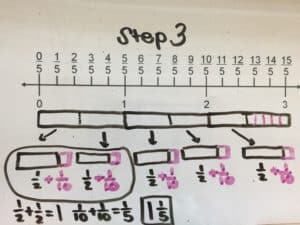
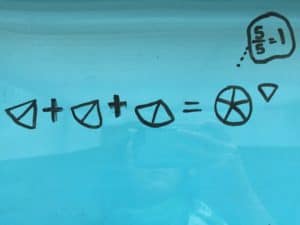We’ll be presenting at the following conferences in April. Stop by and say “I’m a Math Champion” to get one of our cool buttons!

NCSM Annual Conference 2019 | San Diego
April 3 | 1:45 – 2:45 pm
No More “Menacing Multiplication” and “Laborious Long Division” – Understanding Procedures through Number Sense in Grades 3-5
As a mathematics leader, how many times have you heard teachers ask “My students are struggling, can’t I just teach them a procedure?” Teachers recognize the need for students to develop both procedural fluency and conceptual understanding but are often unsure of how to do so. Explore strategies focused on numeracy, sense-making, and fostering a conceptual understanding that will help even the most struggling student understand the abstract algorithms for multiplication and division

NCTM Annual Meeting 2019 | San Diego
We’ll be presenting regular and exhibitor sessions for Singapore Math, Inc. as they’re releasing their new Singapore Math Series Dimensions Math. Come meet the authors!

#133.4 Empowering Algebraic Thinkers
April 4 | 11:00 am – 12:00 pm
Experience how mental math strategies for grades 4–6 build confidence and understanding for future algebra students. Fill up your teaching toolbox with Singapore math strategies that prepare elementary students for advanced math.
#255 Using Mental Math to Deepen Number Sense
April 4 | 3:15 pm – 4:30 pm Beth made some awesome short videos!
#360.3 Ready, Set, Play: Practicing Number Sense with Games
April 5 | 9:30 am – 10:30 am

NCEA 2019 Convention & Expo
Understanding Procedures through Number Sense: Grades 3-5
April 23 | 1:30 PM – 2:45 PM
Join us as we work with manipulatives to understand and practice multi-digit multiplication and long division algorithms for whole numbers and decimals. Learn how to help all learners master the move from concrete to pictorial representation to the ultimate abstract algorithm with a deep understanding of regrouping and place value.
Strategies First: Teaching Fact Fluency with Hands-on Activities and Games
April 24 | 2:00 pm – 3:00 p.m.
If we can’t teach memorization, then what do we do? Participants will learn how to develop hands-on lessons that promote deep conceptual understanding and strengthen students’ number sense. We will explore strategies for teaching and learning addition, subtraction, multiplication, and division facts to make mathematics accessible to all students. Participants will engage in activities and games that promote automaticity with math facts, leaving with the tools needed to take what they learned and apply it immediately in their classrooms.

MCTM Spring Conference 2019
April 25-26, 2019
Ready, Set, Play: Practicing Number Sense with Games
Day/Time TBA