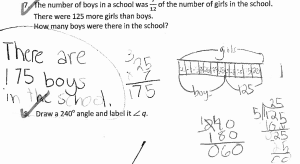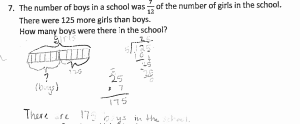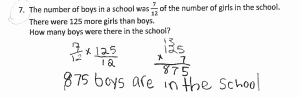For our final post this summer, we thought it would be interesting to look at other challenges schools face in their adoptions. When I re-read a post from the past I always take away something different because I am in a different place with my own experience. Perhaps you are as well!

Direct from the classroom: Challenges & Successes with Singapore Math implementations

Originally published 12/1/2012

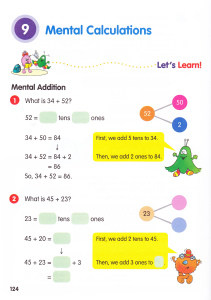
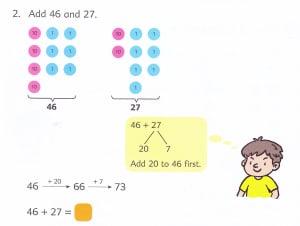
Some teacher challenges & successes with Singapore math one year or three months after adopting the program are below. Click to see larger images.

During follow-up in-services, I like to have teachers meet in grade level groups and spend time discussing the challenges and successes they have had thus far with their teaching of Singapore Math. Each grade level is then asked to list these challenges and successes on a poster and share with the group as a whole. This allows us time to compare and share lessons from the content fresh on their minds.

There is so much challenge the first year when implementing a new curriculum, it’s helpful to take a few moments to reflect on how many successes the teachers and students have had. These posters then guide subsequent teacher learning as we focus on the concepts that they are finding challenging.