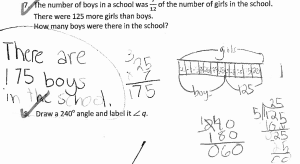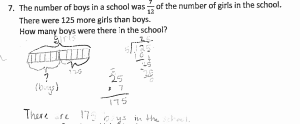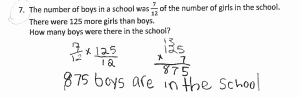Summer’s here, but you’re missing your math? Don’t despair – we’ve got you covered. Check the site each week for one whopper of a word problem that’s sure to challenge!
 This week’s problem comes from Classroom Maths Problem Sums 4 by Casco Publications Pte Ltd
This week’s problem comes from Classroom Maths Problem Sums 4 by Casco Publications Pte Ltd
117 children took part in an art competition. 2/7 the number of girls is equal to 1/3 the number of boys. How many girls took part in the art competition?
Submit your solutions and we’ll post all interesting strategies next week.
Last week’s problem and solution:
3 pears and 4 oranges cost $3.80. If 1 pear and 1 orange together cost $1.10, find the cost of 1 pear.
How did you do?

 This week’s problem comes from New Syllabus Mathematics Strategies Primary 3 by Yee Fook Shiong, published in 2007 by Educational Publishing House Pte Ltd.
This week’s problem comes from New Syllabus Mathematics Strategies Primary 3 by Yee Fook Shiong, published in 2007 by Educational Publishing House Pte Ltd.