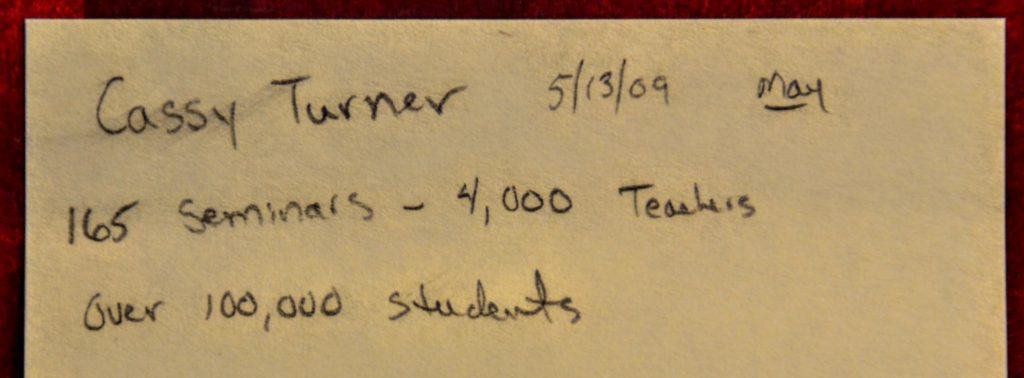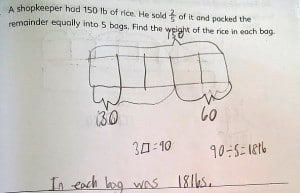In 2008, I left teaching in the classroom to champion Singapore Mathematics and expand its reach to elementary schools and children everywhere. Looking back on the past eight years, I am amazed by the incredible opportunities I’ve had to help schools and teachers make math from Singapore work for every child in every classroom.
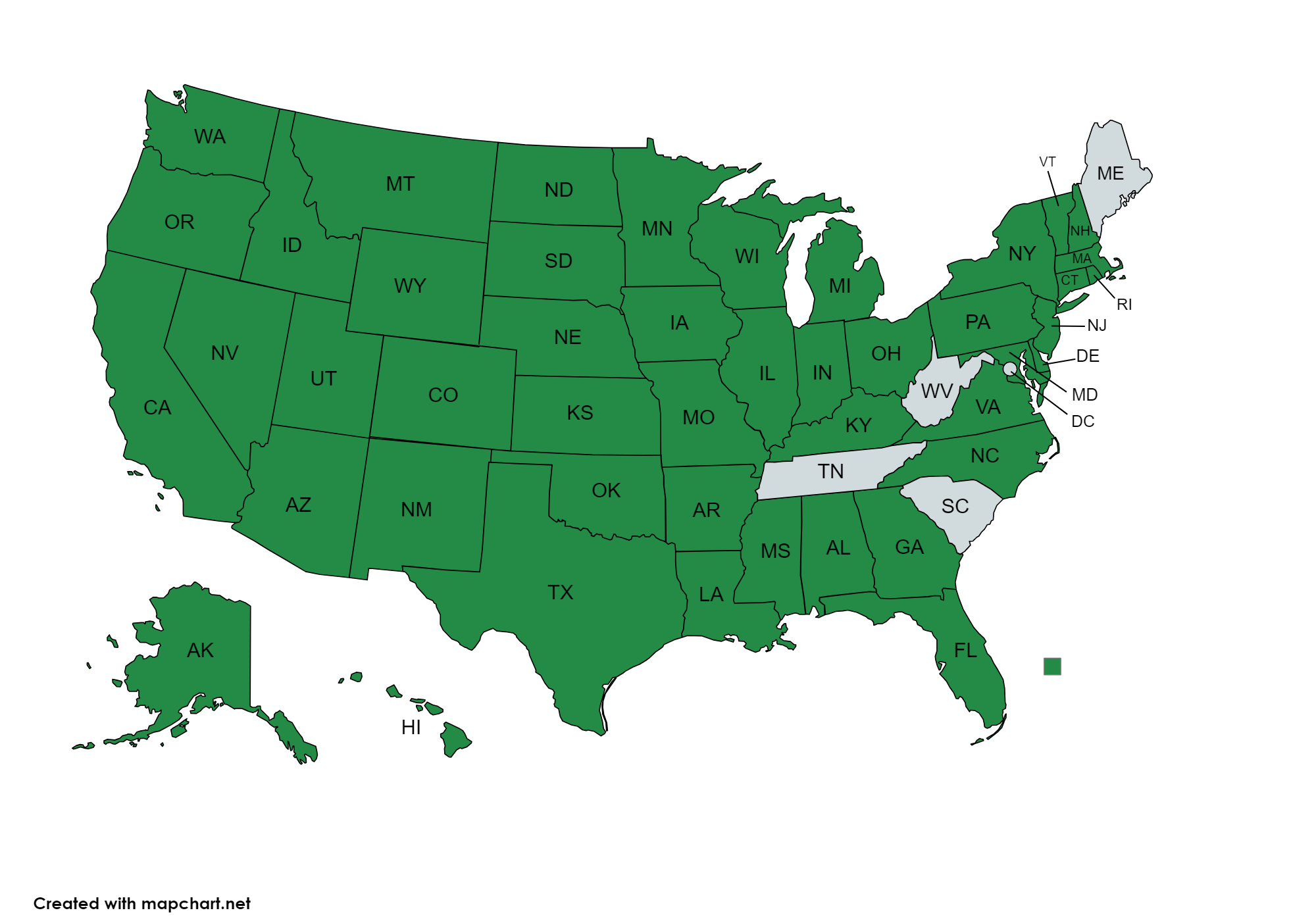
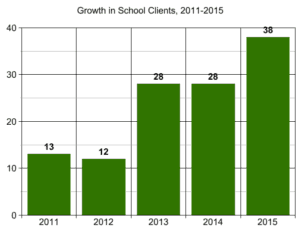 Demand for my training and coaching services has grown every year; recently, it has become impossible to accommodate all the schools looking for help with their math instruction.
Demand for my training and coaching services has grown every year; recently, it has become impossible to accommodate all the schools looking for help with their math instruction.
Expanding has been on my radar for several years, but I did not want growth to affect the quality of professional development services. To take this important step, I needed a candidate who has stellar credentials as a teacher/trainer/coach AND who shares my passion for elementary math.
I’m delighted to share some exciting news. After eight years as a one-person consultancy, I am hiring my first employee.
Introducing Beth Curran
In a 13-year career, Beth Curran has taught mathematics in Kindergarten through 4th Grade as both a classroom teacher and a Singapore Math® specialist. Beth is currently the Lead Math Teacher and Math Department Chair at St. Anne’s-Belfield School, an independent Pre-K-12 school in Charlottesville, Virginia. At St. Anne’s, she oversaw the successful adoption of Primary Mathematics, guiding a team of teachers and partnering with administrators and parents.
Beth wrote about the St. Anne’s implementation here.
What do Beth’s Colleagues say about her impact?
The transition for our faculty to Singapore Math was daunting at first. The unknown can always challenge teachers and schools. Yet, Beth, as a member of a team of newly-minted math specialists, provided key expertise and wise counsel to her colleagues. The result was a palatable sense of relief as the new math vision was manifested daily by strong instruction. She enabled our teachers and school to move confidently in this new direction.
– Fred Chandler, Associate Head of School for Academics, St. Anne’s – Belfield SchoolThere is a depth to Beth Curran’s teaching, and–through her example and through many discussions–she has helped me deepen my own teaching. She prioritizes true mastery of worthy concepts.
– Karen LeMaire, Kindergarten through 4th Grade Math Specialist, St. Anne’s – Belfield School
Beth has provided professional development and ongoing support services to other Virginia schools that have implemented Singapore Math curricula, as well as hosting several informational sessions to schools interested in the Singapore approach. In addition, she has presented at State and regional math educator conferences. Beth is a dedicated, award-winning teacher, presenter, mentor and advocate of making quality mathematics education accessible to all students.
Beth says, “I’m so excited to share all that I’ve learned on my own Singapore Math journey with educators throughout the country, and beyond.”
I’m thrilled that Beth will be joining me in June. Welcome to the team, Beth!
P.S. In addition to hiring Beth, I’ve also formed a new company, Math Champions Professional Development, LLC. More on that development coming soon.