The return from winter break brings with it a refreshed outlook on teaching. Teachers return with an eagerness and enthusiasm for the profession and students return seeming just a little more mature.
Return from winter break also brings with it a sense of urgency. Maybe you’re not as far along in the curriculum as you had hoped. You realize that the frantic push to cover material before break has left students unable to recall content taught. You are feeling the pressure of standardized tests looming.
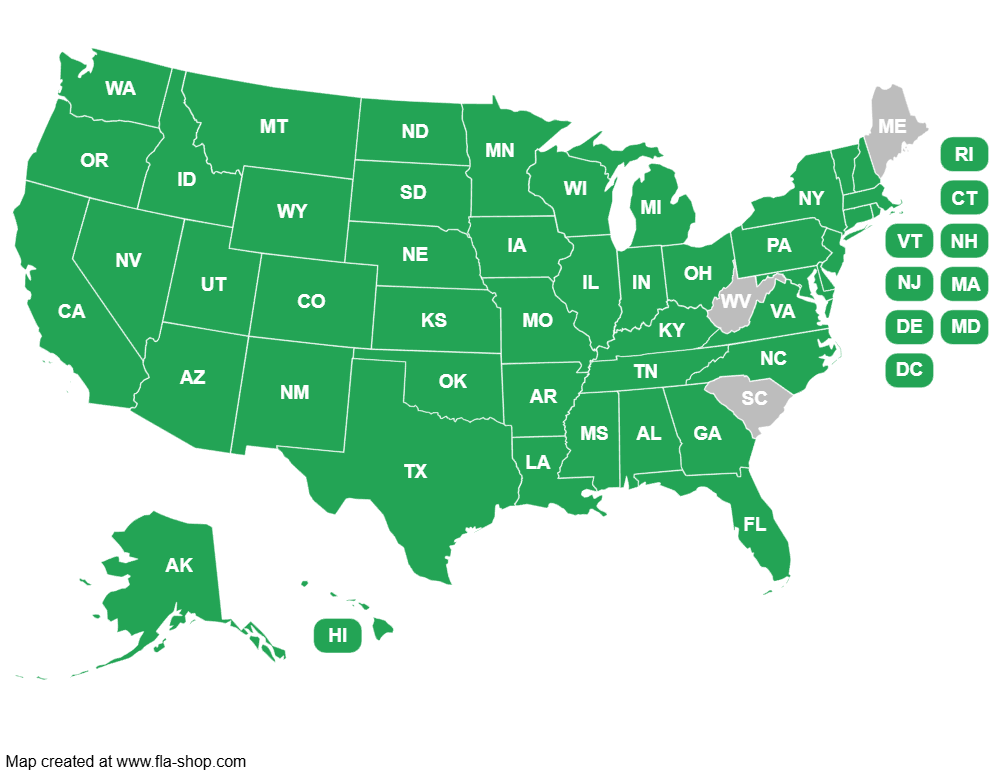
The 2015 TIMSS results were recently published and once again, Eastern Asian countries top the charts. In fact, the gap between the top 5 scoring countries and the United States was 54 points. What sets them apart is their commitment to teaching mathematics at a deep conceptual level with a focus on thinking and problem-solving.
All of that can be very sobering. Take a deep breath and set some goals.
Ask more, tell less
- How do you know that’s correct?
- Are you sure?
- Why does it make sense?
- I wonder why that works.
- Can you solve it in another way?
- Can you build or draw a representation?
- What do you see in your head?
- Can you prove your answer is correct?
- You and your neighbor have different answers, who is correct?
Allow time for understanding
It’s easy this time of year to get caught up in the pressure to cover content, but remind yourself that memorization is not the end goal, understanding is. Taking the time to focus on the concrete-representation-abstract approach will ultimately lead to deep conceptual understanding. Your students (and their test scores) will reap the benefits.
Help students make connections
- How is this like what we just learned?
- Does this remind you of anything?
- Can you make a connection between this and what we have already learned?
By setting a few simple goals, you will set yourself and students up for a successful remainder of the year!





 To approach this lesson with more of an emphasis on inquiry learning, look to the textbook.
To approach this lesson with more of an emphasis on inquiry learning, look to the textbook.
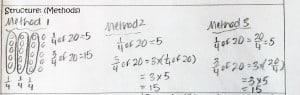 After about five minutes, I gathered the students to share their methods of solving the problem. This is where my direct instruction came in. As students shared their strategies, I organized their independent learning into three methods.
After about five minutes, I gathered the students to share their methods of solving the problem. This is where my direct instruction came in. As students shared their strategies, I organized their independent learning into three methods. Students were then given the task of applying their newly discovered knowledge to solve the problems from the textbook, with my support, if needed.
Students were then given the task of applying their newly discovered knowledge to solve the problems from the textbook, with my support, if needed.