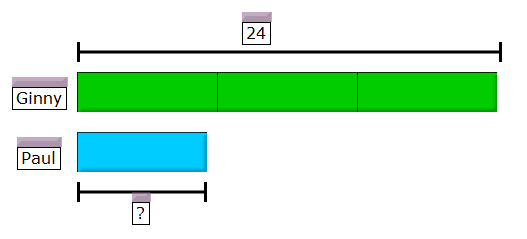
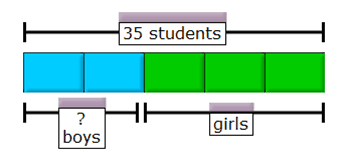
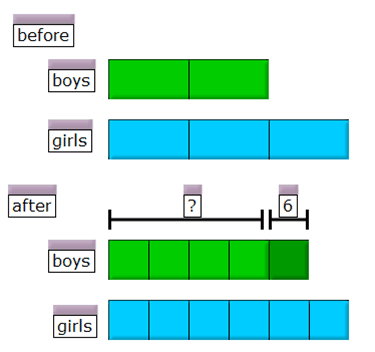
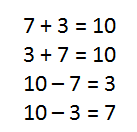Last week I presented with Lauri Susi at the National Council of Teachers of Mathematics (NCTM) 2012 Annual Conference in Philadelphia. Here was our session description:
470 – Technology + Singapore Strategies = Number Sense
Lead Speaker: Cassandra Turner
Co-Speaker: Lauri SusiVisual reasoning is a powerful tool for making sense of mathematics. Learn successful visual strategies and instructional methods from Singapore that allow students to develop a deeper understanding of number concepts using hands-on manipulatives and software. Walk away with strategies for guiding students’ learning that you can use tomorrow.
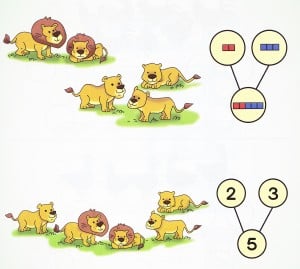
We displayed the above image of lions on the screen while discussing the Concrete-Pictorial-
I don’t like that picture. There are male lions and female lions, they aren’t the same. I can’t add them together and students get confused in upper grades when they think that these can be added.
Which is such a great comment. Why? Because this illustrates one of those interesting points that isn’t always in a student textbook and as the teacher you have to be aware of it : labels matter. Yet it isn’t so obvious at a kindergarten level.
2 male lions and 3 female lions make 5 lions altogether.
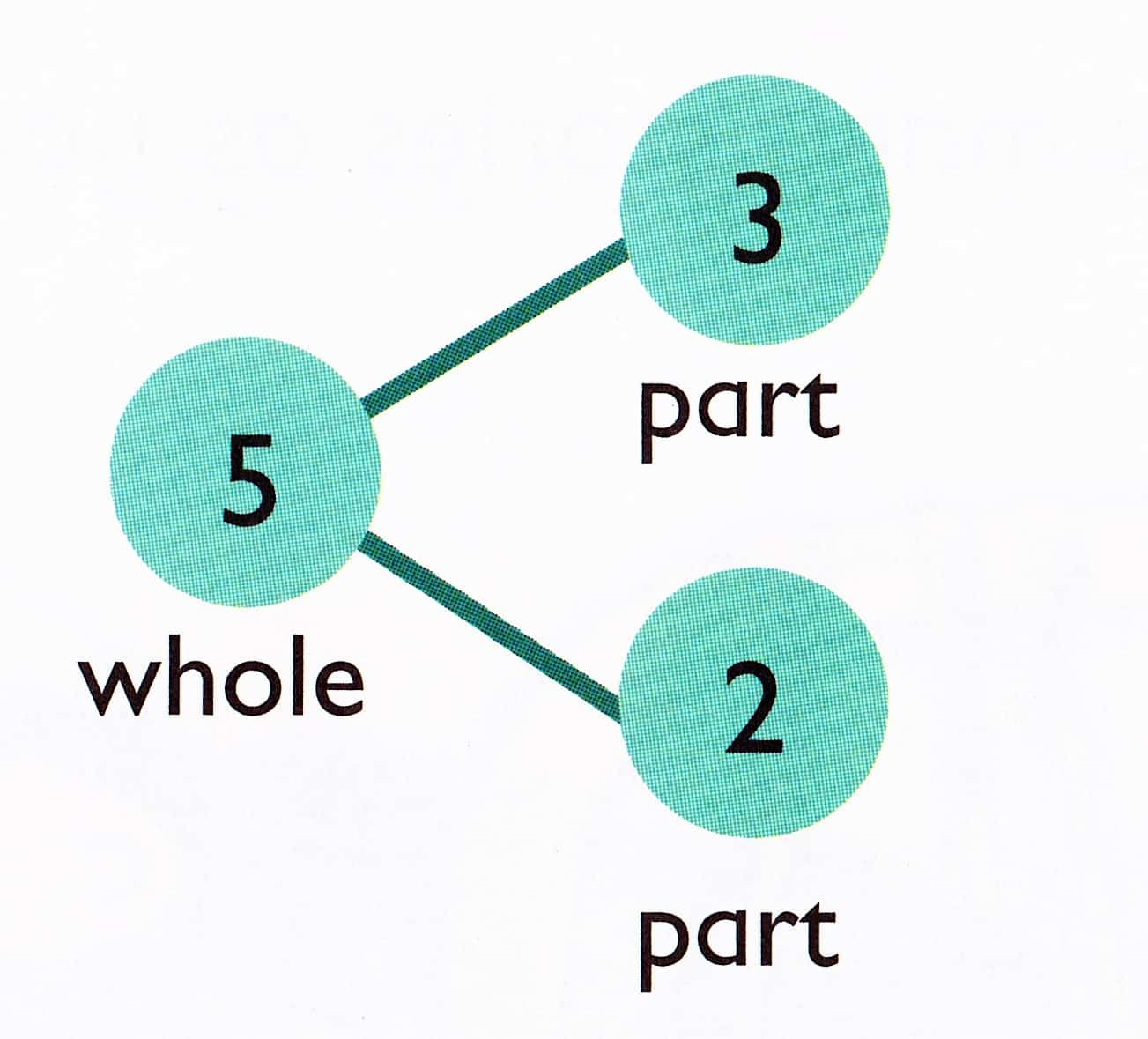
Well, they’re all lions and we’re looking at a part-whole understanding of addition. Here’s another image from the kindergarten book:
2 boys and 3 girls make 5 children.
2 daisies and 2 tulips make 4 flowers.
So how does this apply to later, more advanced concepts? Consider:
- 2 ones and 3 ones make 5 ones.
- 2 tens and 3 tens make 5 tens.
- 2 tens and 3 ones make 23 ones.
- 2 dimes and 3 pennies make 5 coins and they also make 23 cents.
- 2/5 and 3/5 make 5/5
- 2/5 and 3/4 make…hmmm, we need some common terminology here.
Thanks kindergarten and first grade teachers for laying this foundation!