My students love math class. In fact, many will tell you math is their favorite subject. Why? They’ll tell you it’s because Singapore math is fun. I’d say it’s because once they understand how math works, they become confident in their abilities. So what exactly is Singapore math?
Wait, math from Singapore? Isn’t that some little island in Asia?
Primary Mathematics is based on a program of study introduced by the Ministry of Education in Singapore in 1981, a time when Singapore’s students were middling in math. Fifteen years after the adoption of its new Primary Mathematics Syllabus, Singapore students led the world in global Math achievement tests (Singapore topped international rankings first in 1995, and again in 1999, 2003 and 2007).
The Singapore math success story—from mediocre to world-class in a generation—is no secret. The curriculum provides students with a solid foundation in mathematics by focusing on visual understanding, connections, number sense, mastery, and word problems.
Concepts in Singapore Math® are taught in a concrete – pictorial – abstract sequence
Hands-on manipulatives or real life objects are used to demonstrate the concept, then students use and create pictorial representations. This interim visual step is typically missing from many curricula used in the U.S. It provides a transition from the words to an abstract algorithm. The goal is always to use the concrete and visual components to get to a standard algorithm.
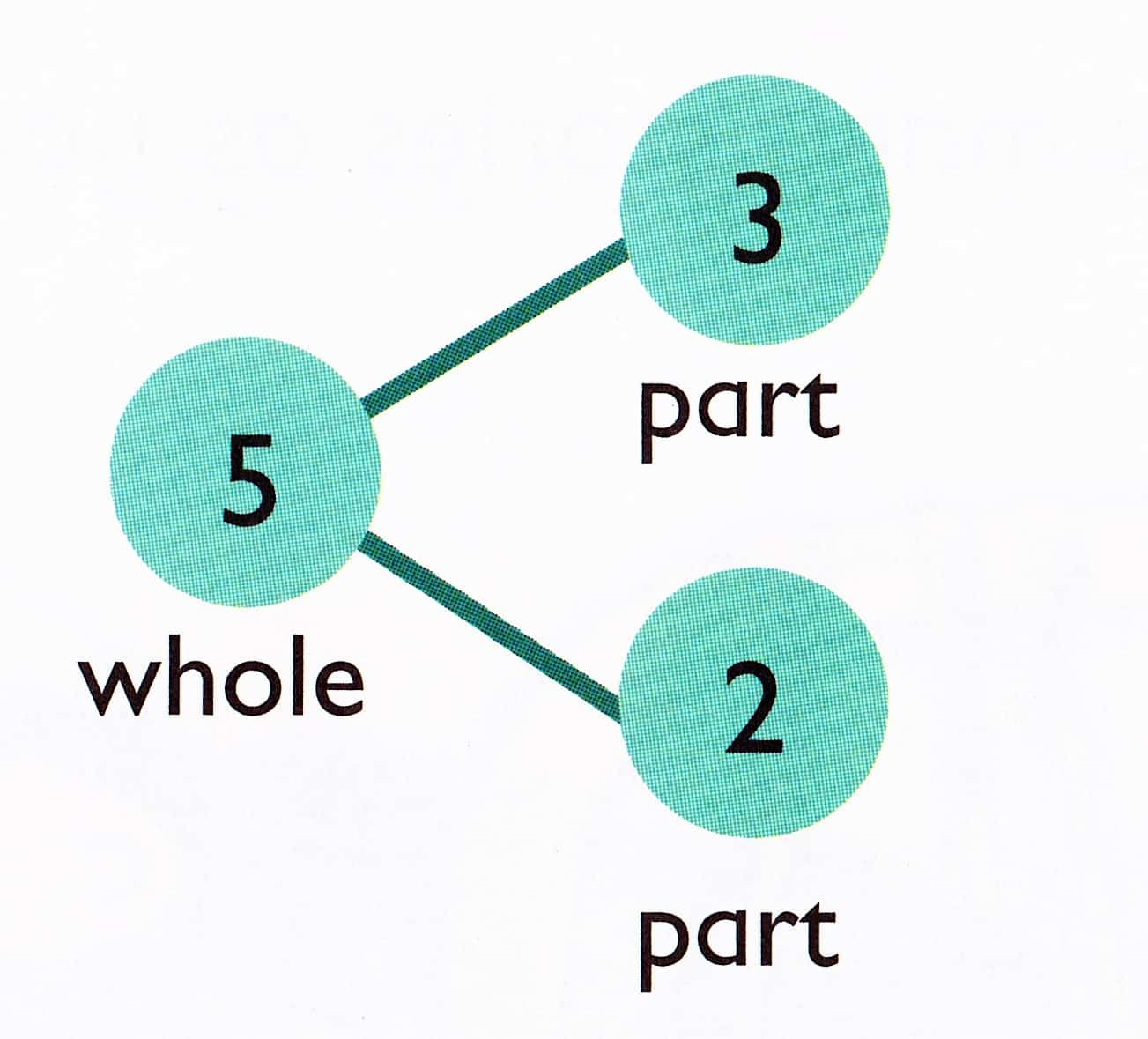
To gain number sense, students are taught to make connections between topics. While first graders will still work on “fact families”, Singapore math also uses a pictorial representation called a “Number Bond” to help students see the connections between addition and subtraction.
Fact Families: Number Bonds:
Understanding numbers and operations is critical to mathematics
Singapore materials focus on place value to provide a deep knowledge of numbers. As students work with and manipulate numbers, they work towards fluency by learning and using mental math strategies.
For example:
“If I know that 7 and 3 make 10, I could solve the problem of 47 + 8 by breaking the number 8 apart into 3 and 5. Adding the 3 to 47 gives me 50, then I can easily add on 5.”
These mental math skills show flexible thinking and provide a “check” students use when the algorithm is learned. I was in a first-grade classroom last week where the teacher was talking about addition and subtraction strategies with her students. They were working with numbers like 9 + 5 and the teacher had asked the students how they got their answers:
“I counted on from 9”
“I took 5 apart to 1 and 4 and made a ten first”
“I used automaticity!”
To get to mastery, students work on focused concepts and skills. U.S. curricula are typically criticized for being “A mile wide and an inch deep”. Topics continually spiral and “It’s ok if kids don’t have their multiplication facts memorized this year, we’ll reteach them again next year.”
And next year and next year…
Not so with schools using Singapore Math®. In first grade, students will learn multiplication of twos and threes within 40. In second grade, they’ll master multiplication and division by 2,3,4,5 and 10. Each year builds on the prior foundation and extends student understanding. By the end of third-grade students will have mastered all of their multiplication tables as well as multiplying and dividing by a single digit. Yep, they will even become proficient with the dreaded “long division algorithm”.
Understanding problem solving
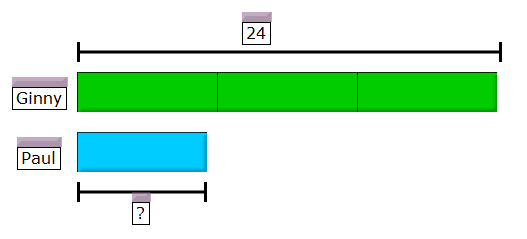
Another component of mastery is the ability to take what you already know and apply it in a new context. Remember being tortured in school with story problems? The heart of the Singapore curriculum is an emphasis on problem-solving — and that means word problems. They are incorporated throughout the materials to provide context to each topic as it’s taught. The key to solving these begins with a bar model or pictorial representation of the word problem. For instance:
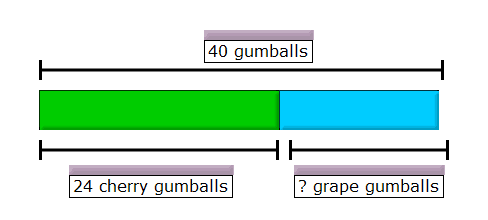
1) Ginny has 40 cherry and grape gumballs in all. She has 24 cherry gumballs. How many grape gumballs does she have?
2) Ginny has 24 gumballs. She has 3 times as many gumballs as Paul does. How many gumballs does Paul have?
3) 2/5 of the students in a class are boys and the rest are girls. There are 35 students in the class. How many boys are in the class?
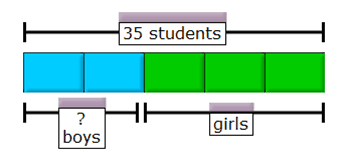
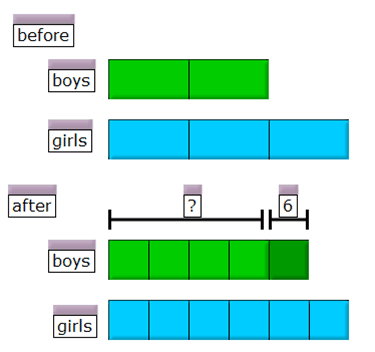
4) The ratio of the number of boys to girls in a class is 2:3. After 6 boys join the class, the ratio becomes 5:6. How many boys were in the class at first?
This is a sixth-grade problem from a unit on changing ratios. Can you see the answer? Note that the number of girls doesn’t change.
1 unit = 6 boys
4 units = 24 boys
Mastering Math Makes Math Fun!
Singapore Math® is a great foundation for elementary math success. Working with teachers in their classrooms, I see the impact the materials have on students every day. Singapore math can help make every child in every classroom a competent and confident mathematics student.
Answers to Word Problems
1) Ginny has 16 grape gumballs
2) Paul has 8 gumballs
3) There are 14 boys in the class
4) There were 24 boys in the class at first
Bar Models generated from ThinkingBlocks.com
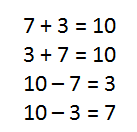


















At 1st grade children and according to 1B TB don’t have to master the multiplication of 2os and 3es
Actually they just learn that multiplication a number by for instant by 5 is like repeating that number 5 times in
The math expreion :
Or
5 times 3 = 3+3+3+3+3
And should use addition skills to to find the sum:
9+3+3= 9+1 +2 +3 = 10+5
= 15
The children do learn also in G2 that :
5×3=3×5
And 5×3 could be expressed as 5+5+5 That to be simpler than adding 5 times 3
Thanks Marwan, You are absolutely correct. Students aren’t expected to master the twos and threes until second grade.
Hi Cassandra
Thank you and thanks to Singapore Math and to all those that are still work hard to give the best to to improve Math education by there exelent website and with exelent , The trainer , you.
Teaching the students how to drow bar model by them self is very important and efficient for simplifying the challenge word problems, for those that express whole-parts word problems when we drow the bar with a length that represents the whole , and befor drowning a bar to represent the given part , then asking is this given part more or less than the middle of the whole as if in ather way we ask where is the middle of the bar that represents the whole,
So 34 = 30+4, half 30 is 15, and half 4 is 2, so half 34 is 17, 18 is the given part so the student will know where to drow it a bit after the middle.
Finding the middle helpe also when approximating to get an estimation.
I know that the students might not anderstand the calculation of finding half of 30 , but if the teacher explains the drawings for each word problem that repeats the same explanation then when time come and they can calculate half of …. Then they will know what to do after that,…
I’ll be delighted to hear your opinion on the importance of teaching the students to drow word problems, and on the way I’m suggesting it.
Half 30 is like half 10 three times,
(Half 10 + half 10 + half 10),and teacher can bring 30 cards and convince student by the concrete manipulation.
So half 34 is half 30 + half 4, it’s 15+2, it’s 17,
The drill 34-18=16 can be done by the whole-part modeling (nomber bond),and if the objective is to find the the nomber then using bond nomber modeling and do the subtraction expression 34-18 by
Mental or by the subtraction algorithm
But if the goal is to start practice model drowning then the steps as explained in previous are appropriate , try it!
And tell me if I’m right.
I’ll be happy if you respond.
Thanks
Marwan
I just can’t let it go!
We can show 17+1 and 17-1, and find the nomber of those particular cards,
The 16.
18 is 1 more than the half so from drown model aviasly anyone can be convinced that the dezird cards is less 1 than 17.
Hi Cassy,
I am preparing for back to school night this coming week and have been searching for a parent’s guide to Singapore Math. And searching. And searching. Your blog post here is closest thing I could find. Is there a way to just get the content of the post so I can make it into a handout? I will share it with you when I am done. Conversely, if you know of a good handout that already exists, if you could share the location, I would really appreciate it!