Over the summer, we thought it would be fun to run some of the most popular posts from the past. It’s mid-July and teachers are already getting ready to go back to school. Here’s an article on planning for the concrete component of a lesson.
Anchor Tasks Demystified
Originally published 2/15/2016
With performance-based standards and 21st-century skill sets teachers are asked to teach mathematics with an emphasis on problems solving and inquiry learning, but how? The answer is simple, with anchor tasks, of course, BUT HOW?
I have attended several seminars and sessions that have done a great job of explaining what an anchor task is and how using anchor tasks can transform my instruction while meeting the needs of all learners. Few, however, have explained how to implement them into my daily lessons. I have been told anchor tasks are right there in the materials, but I have yet to come across a section labeled, “Anchor Task.”
In a recent seminar, hosted by Dr. Yeap Ban Har, I finally got the explanation I had been searching for… I had been looking in the wrong place! Anchor tasks are not found in the Primary Mathematics Teacher’s Guides, but rather in the textbooks.
Dr. Yeap described the evolution of the term on his Facebook page:
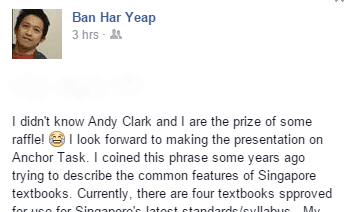
Basically, an Anchor Task is the concrete component of any lesson!
How do I find an Anchor Task?
In Primary Mathematics 4A, Lesson 3.6c (Standards Edition) students will learn to interpret the fraction of a set as a whole number times a fraction. The Teacher’s Guide leads teachers through an effective lesson where the teacher demonstrates how to find 1/3 of 24 using a couple of different methods.
I’ve included links to this same lesson in:
- Primary Mathematics U.S. Edition: Teacher’s Guide | Textbook
- Primary Mathematics Common Core Edition
- Math in Focus – current edition: Part 1 | Part 2
To approach this lesson with more of an emphasis on inquiry learning, look to the textbook.
To create an anchor task, I took the example at the top of the page, find 1/4 of 20, and rewrote it as a word problem. Students worked in partner groups to solve the following: There are 20 M&Ms in a bag. Three friends each eat 1/4 of the bag of M&Ms. How many M&Ms did they eat altogether? Students were asked to find multiple ways of solving the problem and were given 20 chips to use if needed. Because our school has several Math Teachers that teach multiple grades, we devised a lesson planning document. (<-Click for a copy if you’d like to use it to plan your lessons)
As students worked, I circulated around the room and quickly determined which students had mastered how to find 1/4 of 20, which students still needed support with this concept and which students were able to apply that concept to find 3/4 of 20. Were they in the concrete, representational or abstract phase?
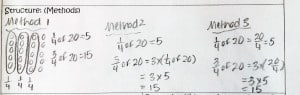After about five minutes, I gathered the students to share their methods of solving the problem. This is where my direct instruction came in. As students shared their strategies, I organized their independent learning into three methods.
I anticipated their strategies in my planning document and during my direct instruction I was sure to include any methods not discovered by my students on their own.
Students were then given the task of applying their newly discovered knowledge to solve the problems from the textbook, with my support, if needed.
The lesson ended with a journal prompt that was closely related to the concept learned.
A well-designed anchor task will engage students in the concrete and representational phases of learning a new concept.
Students will make connections with prior knowledge, reason and think logically to apply what they know to solve a problem with a partner or small group. All students will be given time to work in the concrete phase to develop and hone their conceptual understanding. As students are ready, they will naturally explore the representational or abstract phases of learning and discover strategies, or methods, for solving the given problem. Sharing methods also allows students to communicate mathematically to explain and defend their thinking and consolidate their learning.
