Singapore Mathematics instruction – or, really, just good math instruction – will have students working through three phases of learning, referred to as the Concrete-Pictorial-Abstract approach. In order to teach following this approach, you need to start at the concrete level. Jean Piaget, a Swiss psychologist, believed that in order for students to be able to visualize and abstract mathematics they first must manipulate materials. He called this the concrete operational phase of learning.
So, what do you need to teach concretely? A complete list of recommended materials by grade level can be found here.
Really, though, with a few basic items you can get started…
Linking Cubes
Find linking cubes here.
 Kindergarten – used for counting with one-to-one correspondence, measuring with non-standard units, and for modeling basic addition and subtraction situations.
Kindergarten – used for counting with one-to-one correspondence, measuring with non-standard units, and for modeling basic addition and subtraction situations.
1st – 2nd grade – used for place value understanding, to model story problems and mental math strategies, for measurement with non-standard units, building array models for multiplication, and for beginning bar modeling.
3rd grade – used to model part-whole and comparison word problems involving addition, subtraction, multiplication, and division, for building array models for multiplication and division, and for modeling area.
4th grade and up – used to model word problems for multiplication, division, and ratio, and to model area and volume.
Base-Ten Blocks and Place Value Discs
 Find Base Ten Blocks here and Place Value Discs here.
Find Base Ten Blocks here and Place Value Discs here.
1st grade – Base-Ten Blocks are used to model place value for numbers to 100
2nd grade and up – Place Value Discs are used as a more abstract (and manageable) model for place value understanding for numbers from thousandths to millions, and for modeling and developing a conceptual understanding of the four standard algorithms. Base-Ten blocks can continue to be used for those students needing a one-to-one representation.
Paper Strips and Squares of Equal Size
Cut them from paper found in the recycle bin.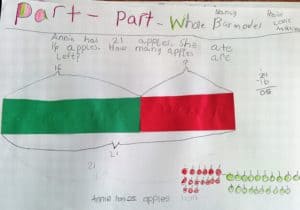
1st and 2nd grade – used to model fractions of a whole.
2nd grade and up – used to model the four operations of fractions with the same size whole and for modeling part-whole and comparison word problems.
Number Cards (Playing Cards) and Dice
 Find number cards on our resources page or pick up some playing cards at your local dollar store. Dice can be found here.
Find number cards on our resources page or pick up some playing cards at your local dollar store. Dice can be found here.
All grades – for playing games and making math fun!
Get creative and have fun building your inventory of math manipulatives!


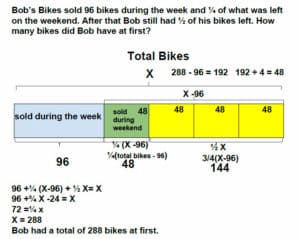



 Recognize the areas within your instruction that were a challenge for you. Maybe your students really struggled with a particular concept or maybe you left a lesson feeling like you needed a do-over. Now is the time to pinpoint those stumbling blocks and think about what support you might need to improve your instruction in those areas. It was my first year teaching a Singapore Math curriculum. With hesitation, I approached a lesson on problem-solving using the bar model. It was a complete flop. Reflecting on it, I realized I hadn’t allowed myself enough time to practice with the bar model and develop the confidence I needed to answer student’s questions on the fly. So, I made a plan to practice bar modeling with Thinking Blocks over the summer. (Thinking Blocks is one of our favorite tools for model drawing. Find an interactive desktop version at
Recognize the areas within your instruction that were a challenge for you. Maybe your students really struggled with a particular concept or maybe you left a lesson feeling like you needed a do-over. Now is the time to pinpoint those stumbling blocks and think about what support you might need to improve your instruction in those areas. It was my first year teaching a Singapore Math curriculum. With hesitation, I approached a lesson on problem-solving using the bar model. It was a complete flop. Reflecting on it, I realized I hadn’t allowed myself enough time to practice with the bar model and develop the confidence I needed to answer student’s questions on the fly. So, I made a plan to practice bar modeling with Thinking Blocks over the summer. (Thinking Blocks is one of our favorite tools for model drawing. Find an interactive desktop version at  As you pack up your room and head off into summer bliss, know that you will return to the new school year with an awareness of all that you gained by reflecting on your practice.
As you pack up your room and head off into summer bliss, know that you will return to the new school year with an awareness of all that you gained by reflecting on your practice.