Summer’s here, but you’re missing your math? Don’t despair – we’ve got you covered. Check the site each week for one whopper of a word problem that’s sure to challenge!
This week’s problem comes from Math in Focus Enrichment 4A by Ang Kok Cheng, published in 2015 by Marshall Cavendish International (Singapore) Private Limited.
Two plates and 3 bowls weigh 2 1/5 lbs. Five plates and 6 bowls weigh 4 9/10 lbs. Find the weight of one plate.
Submit your solutions and we’ll post all interesting strategies next week.
Last week’s problem and solution:
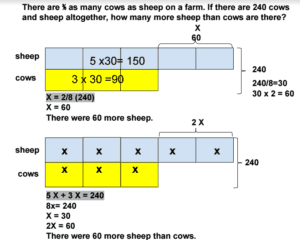
A grocer sold a carton of apples to some customers. The first customer tasted one apple and bought half the remaining apples. The second and third customers did the same. The fourth customer also tasted one apple and bought the remaining 23 apples. How many apples were there in the carton at first?
Whew! How did you do?
Once again, reader Shirley Davis submitted a solution:


 To approach this lesson with more of an emphasis on inquiry learning, look to the textbook.
To approach this lesson with more of an emphasis on inquiry learning, look to the textbook.
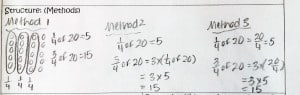 After about five minutes, I gathered the students to share their methods of solving the problem. This is where my direct instruction came in. As students shared their strategies, I organized their independent learning into three methods.
After about five minutes, I gathered the students to share their methods of solving the problem. This is where my direct instruction came in. As students shared their strategies, I organized their independent learning into three methods. Students were then given the task of applying their newly discovered knowledge to solve the problems from the textbook, with my support, if needed.
Students were then given the task of applying their newly discovered knowledge to solve the problems from the textbook, with my support, if needed.