Over the summer, we thought it would be fun to run some of the most popular posts from the past. When I re-read a post from the past I always take away something different because I am in a different place with my own experience. Perhaps you are as well!
Learning from the East: The benefits of persistence
Originally published 1/13/13
Working with schools, teachers, and parents over the last five years, I’m often asked whether cultural differences can explain why Singapore’s students have led the world in international math standings for 15 years while US students rank no better than mid-pack.
When I visited Singapore in 2007, I learned how the country decided to focus on building strong Singaporean citizens beginning with their earliest education. The country’s mathematics curriculum (Primary Mathematics) was developed in the early 1980s with this goal in mind. At that time, Singapore’s students were mediocre at math. Within a few years after the launch of the second edition of Primary Mathematics, Singapore’s students topped the international TIMSS study.
To me, it’s quite easy to attribute much of Singapore’s Math success to changes in how it approached education, including, most importantly, the new curriculum. Could Singapore’s culture have changed dramatically between 1984 (when Singapore’s students were ranked 16th of 26 in the Second International Science Study) and 1995 (when they ranked first in the TIMSS study)?
Today, much attention is paid to “Tiger Mothers,” who, in the words of the Economist,
“load their cubs down with extra homework and tuition to make them excel at school.”
This trend seems more recent; it’s also one which, remarkably, Singapore’s current Prime Minister wants to curtail (http://www.economist.com/
A more subtle consideration concerns expectations; how do parents and teachers ask students to engage in schoolwork?
I had a driveway moment this fall when NPR ran a story (http://www.npr.org/blogs/
“For the most part in American culture, intellectual struggle in schoolchildren is seen as an indicator of weakness, while in Eastern cultures it is not only tolerated but is often used to measure emotional strength.”
Reporter Spiegel then chooses to NOT to choose between East and West. In this silence, though, I believe there is a teachable moment for those of us in the West.
In training sessions with teachers, it is not uncommon to encounter resistance when I advise (insist) that teachers give students the opportunity to really work on math problems. This can be a difficult skill for teachers to learn.
And if teachers are inclined to want to move their class along before giving students a chance to truly work the math, parents can worse. They are unaccustomed to and uncomfortable at seeing their children struggle, unable to finish their home enjoyment (aka homework). Parents sometimes can be too quick to either give their kids a pass (well, you have tried, haven’t you?) or demand an explanation of the teacher (why can’t my child do the homework?).
Here’s where I find that it’s critical to have laid the groundwork and properly set expectations. Teachers need patience (whew, do teachers ever need patience!). They must let their students work through problems, even if they end up struggling and having to start over. And parents need to appreciate that homework (honestly completed or struggled with) can be the best feedback loop for teachers.
Pointing at cultural differences to rationalize a lack of math proficiency in many of our students serves no one. Instead, I think there’s a lot to be gained by asking that western students work a bit more to earn some of the praise they frequently receive.
To approach this lesson with more of an emphasis on inquiry learning, look to the textbook.
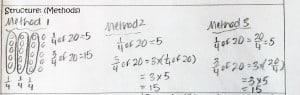After about five minutes, I gathered the students to share their methods of solving the problem. This is where my direct instruction came in. As students shared their strategies, I organized their independent learning into three methods.
Students were then given the task of applying their newly discovered knowledge to solve the problems from the textbook, with my support, if needed.
