This article originally was featured in the fall 2018 issue of St. Anne’s-Belfield School’s Perspectives magazine and is republished with both the school and author’s permission.
The author, Sara Kronstain, has almost a decade of experience guiding elementary and middle school mathematicians to become critical thinkers and problem solvers. She teaches fifth-grade math and is the Kindergarten-6th Grade Math Department Chair at St. Anne’s-Belfield School in Charlottesville, Virginia.
Problem-Solving: The Heart of Singapore Math
When I was in school, my math classes were typical of what one would expect a “traditional” math class to look like. I remember sitting in my elementary and middle school classes, watching as my teachers modeled problem after problem. The class would listen and then practice many of the same types of problems in our notebooks. While this type of teaching may achieve the immediate goal of learning a mathematical procedure, it does not guide students to reach an integral part of learning mathematics: problem-solving (Cai & Lester, 2010).
Singapore Math is comprised of a framework with problem-solving being the center of learning mathematics. This framework is built around five key components – metacognition, process, attitudes, skills, and concepts – all being of equal importance in developing mathematical problem solving in students. Whereas traditional math classes may place primary importance on developing skills and concepts in students, the additional three components of metacognition (self-regulation of learning), process (reasoning, making connections, and applying knowledge), and attitudes (perseverance, confidence, interest) are all key to developing critical thinking and problem solving skills in students (Ministry of Education Singapore, 2006).
A typical Singapore Math lesson is taught with a concrete-pictorial-abstract approach. Where many of my lessons as a math student began in the abstract stage (solving equations), the concrete and pictorial stages allow students to create and solidify their own understanding of a topic. The concrete stage refers to using hands-on materials to model a mathematical situation. The pictorial stage consists of diagrams and other visuals, thus building students’ learning in a tangible way (Maths No Problem!, 2018). The concrete and pictorial stages allow students to understand why math works the way it does before learning the procedure of how to solve using an algorithm.
Most Singapore Math lessons begin with an anchor task, allowing students to explore these three stages. The anchor task is a question that allows students the chance to deeply explore a topic and develop multiple methods for solving a problem (Ban Har, 2013). Let us say, for example, a group of fifth graders were posed the problem, “The distance of a race is 3km. Lily ran two-fifths of the distance. How many kilometers did Lily run?” Students would be given the opportunity to freely explore this question by using manipulatives such as fraction bars, fractions circles, or paper (for folding) along with writing materials. Here are a few examples of possible student responses to this question:
Method: Repeated Addition
Add ⅖ + ⅖ + ⅖. Students may use fraction bars, fraction circles, or pictures. Students become familiar with the phrase “3 groups of ⅖”.

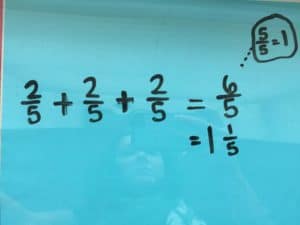
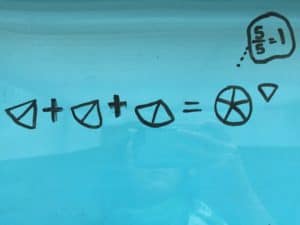

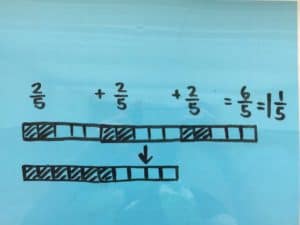
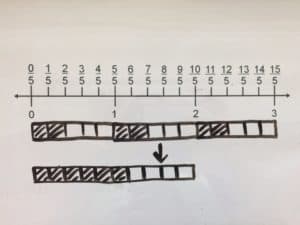
Method: Bars
Three boxes are each split into fifths. Two of each of the fifths in all three boxes are shaded in. The shaded parts are added together.

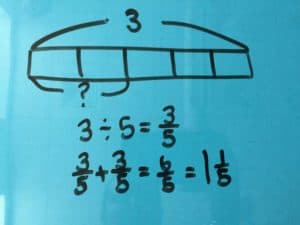
Method: Bar Model
A bar with the length of 3 wholes can be split into five parts. Each part has a value of ⅗. Then add ⅗ + ⅗ .
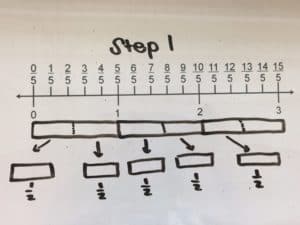
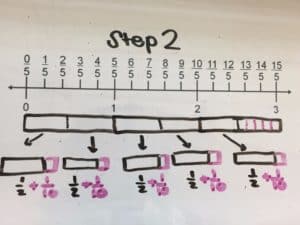
Method: Addition with Fractions
Three boxes are split into 5 equal groups, first by placing one half in each group. Then, split the leftover half into five parts (tenths). Each group will have one half of a whole and one tenth of a whole. Combine two groups by adding two halves to two tenths.
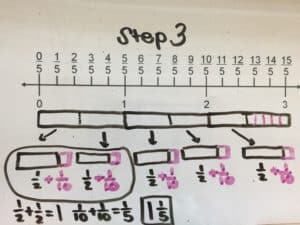
In this example, the repeated addition method reinforces addition with fractions, while the last method has students thinking about and manipulating fractions in a much more complex way. Thinking back to the five key components of Singapore Math, students in this example are refining their process of learning operations with fractions by making connects across operations. It is powerful that these responses are coming from students, as they are building their understanding of math through collaboration with their peers. In sharing methods, listening to other’s methods, and processing others methods, students are also developing their metacognition. This question could also be modified and challenge students to problem solve in an even deeper way. “What if the total distance was ½ km? What if the total distance was 3 ½ km?” Students can then go back to the concrete, pictorial, and abstract stages and continue to build on their problem-solving abilities.
At the end of the day the primary purpose of this math lesson, or any math lesson for that matter, is not simply to learn how to multiply fractions by a whole number. The most important takeaways are the critical thinking, questioning, collaboration, and problem-solving that happens among students. Teachers are not preparing students to go out into a world where they will simply be asked to recite an algorithm. While a goal is for each child to develop a deep love of math, the biggest hope is that students learn to ask questions, logically think through problems, and make sense of the world around them.
References
Ban Har, Yeap. (2013, June 13). Singapore Math at the Blake School, Hopkins, MN. Retrieved from http://banhar.blogspot.com/search?q=anchor+task
Cai, Jinfa, & Lester, Frank. (2010, April 8). Problem Solving. National Council of Teachers of Mathematics. Retrieved from https://www.nctm.org/Research-and-Advocacy/Research-Brief-and-Clips/Problem-Solving/#brief
Kaur, Berinderjeet. (2018, March 29). Building the Maths house: Singapore’s curriculum framework. Oxford Education Blog. Retrieved from https://educationblog.oup.com/secondary/maths/building-the-maths-house-singapores-curriculum-framework
Ministry of Education Singapore. (2006). Mathematics Syllabus Primary. Retrieved from https://www.moe.gov.sg/docs/default-source/document/education/syllabuses/sciences/files/2007-mathematics-%28primary%29-syllabus.pdf
Maths No Problem! (2018). Concrete Pictorial Abstract. Retrieved from https://mathsnoproblem.com/en/the-maths/teaching-methods/concrete-pictorial-abstract/